
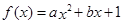 在
在 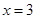 處的切線方程為
處的切線方程為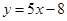 .
.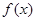 的解析式;
的解析式;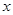 的方程
的方程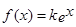 恰有兩個不同的實根,求實數(shù)
恰有兩個不同的實根,求實數(shù)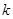 的值 ;
的值 ; 滿足
滿足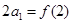 ,
, ,求
,求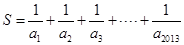 的整數(shù)部分.
的整數(shù)部分. 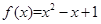 .(2)
.(2) 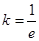 或
或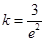 (3)
(3)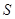 的整數(shù)部分為. l4分
的整數(shù)部分為. l4分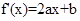 , 1分
, 1分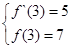 ,即
,即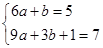 , 2分
, 2分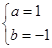 3分
3分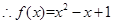 . 4分
. 4分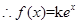 ,即
,即 ,得
,得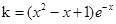 , ………5分
, ………5分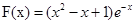 ,
,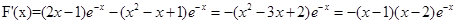 . ……6分
. ……6分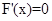 ,得
,得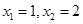 ………7分
………7分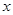 變化時,
變化時,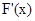 、
、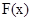 的變化情況如下表:
的變化情況如下表: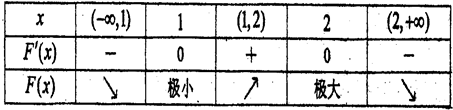
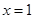 時,F(xiàn)(x)取極小值
時,F(xiàn)(x)取極小值 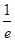 ;當
;當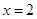 時,F(xiàn)(x)取極大值
時,F(xiàn)(x)取極大值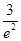 …………8分
…………8分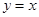 和函數(shù)
和函數(shù)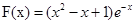 的大致圖象,可知當
的大致圖象,可知當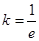 或
或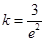 時,
時,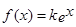 恰有兩個不同的實根, ………9分
恰有兩個不同的實根, ………9分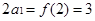 ,得
,得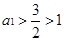 ,又
,又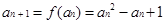 。
。 ,
,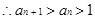 . 10分
. 10分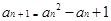 ,得
,得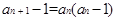 , 11分
, 11分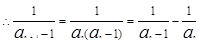 ,即
,即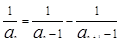 12分
12分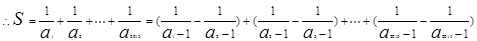
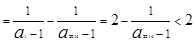
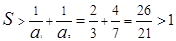 13分
13分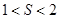 ,故
,故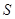 的整數(shù)部分為. l4分
的整數(shù)部分為. l4分

 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源:不詳 題型:單選題
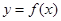 ,如果存在區(qū)間
,如果存在區(qū)間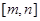 ,同時滿足下列條件:①
,同時滿足下列條件:①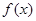 在
在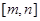 內(nèi)是單調(diào)的;②當定義域是
內(nèi)是單調(diào)的;②當定義域是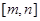 時,
時,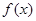 的值域也是
的值域也是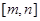 ,則稱
,則稱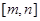 是該函數(shù)的“夢想?yún)^(qū)間”.若函數(shù)
是該函數(shù)的“夢想?yún)^(qū)間”.若函數(shù)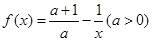 存在“夢想?yún)^(qū)間”,則
存在“夢想?yún)^(qū)間”,則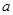 的取值范圍是( )
的取值范圍是( )A.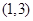 | B.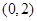 | C.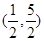 | D.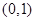 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
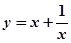 在
在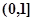 上是減函數(shù),在
上是減函數(shù),在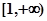 上是增函數(shù);
上是增函數(shù);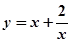 在
在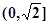 上是減函數(shù),在
上是減函數(shù),在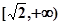 上是增函數(shù);
上是增函數(shù);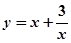 在
在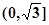 上是減函數(shù),在
上是減函數(shù),在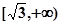 上是增函數(shù);
上是增函數(shù);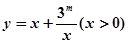 的值域是
的值域是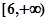 ,則實數(shù)
,則實數(shù)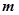 的值是 .
的值是 .查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
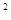 -2s) ≥-f(2t-t
-2s) ≥-f(2t-t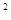 ),則
),則| A.s≥t | B.s<t | C.|s-1|≥|t-1| | D.s+t≥0 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
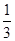 )的值;
)的值;查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com