
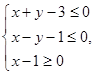 ,O為坐標原點,定點A(6,8),則
,O為坐標原點,定點A(6,8),則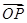 在
在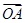 上的投影的范圍
上的投影的范圍A.[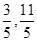 ] ] | B.[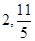 ] ] | C.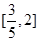 | D.[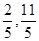 ] ] |
 .
.

 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源:不詳 題型:單選題
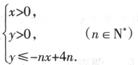 表示的平面區域為Dn an表示區域Dn中整點的個數(其中整點是指橫、縱坐標都是整數的點),則
表示的平面區域為Dn an表示區域Dn中整點的個數(其中整點是指橫、縱坐標都是整數的點),則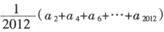 =
=| A.1012 | B.2012 | C.3021 | D.4001 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com