
【題目】在平面四邊形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,將△ABD沿BD折起,使得平面ABD⊥平面BCD,如圖. 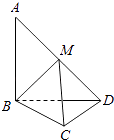
(1)求證:AB⊥CD;
(2)若M為AD中點,求直線AD與平面MBC所成角的正弦值.
【答案】
(1)證明:∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB平面ABD,AB⊥BD,
∴AB⊥平面BCD,又CD平面BCD,∴AB⊥CD
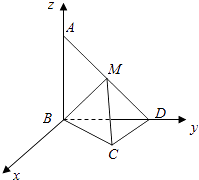
(2)解:建立如圖所示的空間直角坐標系.
∵AB=BD=CD=1,AB⊥BD,CD⊥BD,
∴B(0,0,0),C(1,1,0),A(0,0,1),D(0,1,0),M ![]() .
.
∴ ![]() =(0,1,﹣1),
=(0,1,﹣1), ![]() =(1,1,0),
=(1,1,0), ![]() =
= ![]() .
.
設平面BCM的法向量 ![]() =(x,y,z),則
=(x,y,z),則 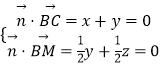 ,
,
令y=﹣1,則x=1,z=1.
∴ ![]() =(1,﹣1,1).
=(1,﹣1,1).
設直線AD與平面MBC所成角為θ.
則sinθ=|cos ![]() |=
|= 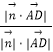 =
= ![]() =
= ![]() .
.
【解析】(1)利用面面垂直的性質定理即可得出;(2)建立如圖所示的空間直角坐標系.設直線AD與平面MBC所成角為θ,利用線面角的計算公式sinθ=|cos ![]() |=
|= 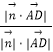 即可得出.
即可得出.
【考點精析】本題主要考查了空間中直線與直線之間的位置關系和空間角的異面直線所成的角的相關知識點,需要掌握相交直線:同一平面內,有且只有一個公共點;平行直線:同一平面內,沒有公共點;異面直線: 不同在任何一個平面內,沒有公共點;已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則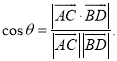 才能正確解答此題.
才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】學校計劃在全國中學生田徑比賽期間,安排6位志愿者到4個比賽場地提供服務,要求甲、乙兩個比賽場地各安排一個人,剩下兩個比賽場地各安排兩個人,其中的小李和小王不在一起,不同的安排方案共有( )
A. 168種 B. 156種 C. 172種 D. 180種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究高中學生對鄉村音樂的態度(喜歡和不喜歡兩種態度)與性別的關系,運用2×2列聯表進行獨立性檢驗,經計算K2=8.01,附表如下:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
參照附表,得到的正確的結論是( )
A. 有99%以上的把握認為“喜歡鄉村音樂與性別有關”
B. 有99%以上的把握認為“喜歡鄉村音樂與性別無關”
C. 在犯錯誤的概率不超過0.1%的前提下,認為“喜歡鄉村音樂與性別有關”
D. 在犯錯誤的概率不超過0.1%的前提下,認為“喜歡鄉村音樂與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,有兩條相交成60°角的直線![]() ,交點為
,交點為![]() .甲、乙分別在
.甲、乙分別在![]() 上,起初甲離
上,起初甲離![]() 點
點![]() ,乙離
,乙離![]() 點
點![]() ,后來甲沿
,后來甲沿![]() 的方向,乙沿
的方向,乙沿![]() 的方向,同時以
的方向,同時以![]() 的速度步行.求:
的速度步行.求:

(1)起初兩人的距離是多少?
(2)![]() 后兩人的距離是多少?
后兩人的距離是多少?
(3)什么時候兩人的距離最短?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有兩位射擊運動員在一次射擊測試中各射靶7次,每次命中的環數如下:
甲 7 8 10 9 8 8 6 乙 9 10 7 8 7 7 8
則下列判斷正確的是( )
A. 甲射擊的平均成績比乙好 B. 甲射擊的成績的眾數小于乙射擊的成績的眾數
C. 乙射擊的平均成績比甲好 D. 甲射擊的成績的極差大于乙射擊的成績的極差
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一位數學老師在黑板上寫了三個向量![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 都是給定的整數.老師問三位學生這三個向量的關系,甲回答:“
都是給定的整數.老師問三位學生這三個向量的關系,甲回答:“![]() 與
與![]() 平行,且
平行,且![]() 與
與![]() 垂直”,乙回答:“
垂直”,乙回答:“![]() 與
與![]() 平行”,丙回答:“
平行”,丙回答:“![]() 與
與![]() 不垂直也不平行”,最后老師發現只有一位學生判斷正確,由此猜測
不垂直也不平行”,最后老師發現只有一位學生判斷正確,由此猜測![]() ,
,![]() 的值不可能為( )
的值不可能為( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
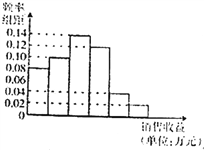
【題目】某公司為了解廣告投入對銷售收益的影響,在若干地區各投入![]() 萬元廣告費用,并將各地的銷售收益(單位:萬元)繪制成如圖所示的頻率分布直方圖.由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從
萬元廣告費用,并將各地的銷售收益(單位:萬元)繪制成如圖所示的頻率分布直方圖.由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從![]() 開始計數的.
開始計數的.
廣告投入 | 1 | 2 | 3 | 4 | 5 |
銷售收益 | 2 | 3 | 2 | 5 | 7 |
(Ⅰ)根據頻率分布直方圖計算圖中各小長方形的寬度;
(Ⅱ)該公司按照類似的研究方法,測得另外一些數據,并整理得到上表:
表中的數據顯示![]() 與
與![]() 之間存在線性相關關系,求
之間存在線性相關關系,求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(Ⅲ)若廣告投入![]() 萬元時,實際銷售收益為
萬元時,實際銷售收益為![]() 萬元,求殘差
萬元,求殘差![]() .
.
附: ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com