【答案】
分析：切和弦共同存在的等式中，一般要切化弦，根據兩外項之積等于兩內項之積，把分式化為整式，移項，逆用兩角和的余弦公式，把腳C化為A+B用兩角和的余弦公式展開，合并同類項，得到兩角余弦乘積為零，則兩角中必有一個直角．
解答：解：由已知得：
，
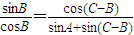
∴sinAsinB+sinBsin（C-B）=cosBcos（C-B），
移項，逆用兩角和的余弦公式得：
sinAsinB=cosC，
∵在△ABC中，cosC=-cos（A+B），
∴sinAsinB=-cos（A+B），
∴cosAcosB=0，γ
∴cosA=0或 cosB=0，
∴△ABC是直角三角形．
點評：和三角形有關的三角恒等變形，要求能用所有的公式特別是余弦的和差角公式 進行簡單的三角函數式的化簡、求值及恒等式的證明
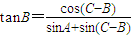，試判斷△ABC的形狀．
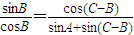