【答案】
分析:(Ⅰ)由數列{a
n+λn
2+μn}為等比數列得到當q≠0時,a
n+1+λ(n+1)
2+μ(n+1)=q(a
n+λn
2+μn)對?n∈N
*成立,然后把a
n+1=2a
n-n
2+3n,代入得到①,所以根據多項式為0的條件解出λ、μ、q的值即可;
(Ⅱ)由(Ⅰ)得到a
n的通項,代入得到b
n的通項,然后根據
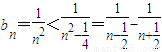
列舉s
n得到s
n<

(1);然后再利用

n(n+1)(2n+1)s
n=(1
2+2
2+3
2+…+n
2)(
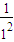
+
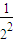
+
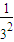
+…+
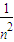
)>(1+1+1+…+1)
2(n個1)=n
2即得到
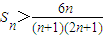
(2),綜合(1)(2)得證.
解答:解:(Ⅰ)若{a
n+λn
2+μn}為等比數列,
則存在q≠0,使a
n+1+λ(n+1)
2+μ(n+1)=q(a
n+λn
2+μn)對?n∈N
*成立.
由已知:a
n+1=2a
n-n
2+3n,代入上式,
整理得(q-2)a
n+(λq-λ+1)n
2+(μq-2λ-μ-3)n-λ-μ=0①
∵①式對?n∈N
*成立,
∴
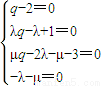
解得
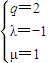
∴當λ=-1,μ=1時,數列{a
n+λn
2+μn}是公比為2的等比數列;
(Ⅱ)證明:由(Ⅰ)得:a
n-n
2+n=(a
1-1
2+1)•2
n-1,即a
n=2
n-1+n
2-n
所以
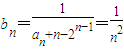
∵
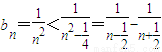
n≥2時,s
n=b
1+b
2+b
3+…+b
n<1+
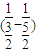
+
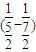
+…+
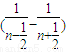
=

(1)
現證:
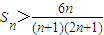
(n≥2)
n≥2時,

n(n+1)(2n+1)s
n=(1
2+2
2+3
2+…+n
2)(
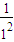
+
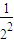
+
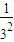
+…+
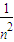
)>(1+1+1+…+1)
2(n個1)=n
2∴
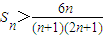
(2)
根據(1)(2)可知

>
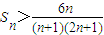
對于n≥2,n∈N
*都成立.
點評:考查學生會根據已知條件判斷數列是等比數列,會利用數列求和的方法證明不等式.

 ,Sn為數列{bn}的前n項和,證明:n≥2時,
,Sn為數列{bn}的前n項和,證明:n≥2時,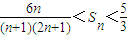 .
.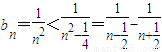 列舉sn得到sn<
列舉sn得到sn< (1);然后再利用
(1);然后再利用 n(n+1)(2n+1)sn=(12+22+32+…+n2)(
n(n+1)(2n+1)sn=(12+22+32+…+n2)(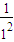 +
+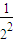 +
+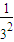 +…+
+…+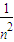 )>(1+1+1+…+1)2(n個1)=n2即得到
)>(1+1+1+…+1)2(n個1)=n2即得到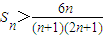 (2),綜合(1)(2)得證.
(2),綜合(1)(2)得證.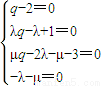
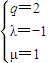
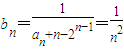
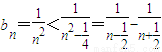
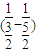 +
+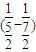 +…+
+…+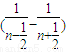 =
= (1)
(1)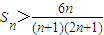 (n≥2)
(n≥2) n(n+1)(2n+1)sn=(12+22+32+…+n2)(
n(n+1)(2n+1)sn=(12+22+32+…+n2)(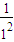 +
+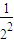 +
+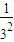 +…+
+…+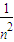 )>(1+1+1+…+1)2(n個1)=n2
)>(1+1+1+…+1)2(n個1)=n2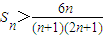 (2)
(2) >
>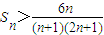 對于n≥2,n∈N*都成立.
對于n≥2,n∈N*都成立.
