
【題目】定義函數F(a,b)= ![]() (a+b﹣|a﹣b|)(a,b∈R),設函數f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函數F(f(x),g(x))的最大值與零點之和為( )
(a+b﹣|a﹣b|)(a,b∈R),設函數f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函數F(f(x),g(x))的最大值與零點之和為( )
A.4
B.6
C.![]()
D.![]()
【答案】B
【解析】解:∵F(a,b)= ![]() (a+b﹣|a﹣b|)=
(a+b﹣|a﹣b|)= ![]() ,
,
∴設G(x)=F(f(x),g(x))= ![]() .
.
∵當﹣1≤x≤2時,f(x)≥g(x),此時G(x)=x+2∈[1,4],
此時函數無零點,此時最大值為4,
當x>2或x<﹣1時,f(x)<g(x),G(x)=﹣x2+2x+4=﹣(x﹣1)2+3<4,
綜上可得,函數G(x)的最大值為4,
由G(x)=﹣x2+2x+4=0,得方程的兩根之和為2,
則函數F(f(x),g(x))的最大值與零點之和為2+4=6,
故選:B.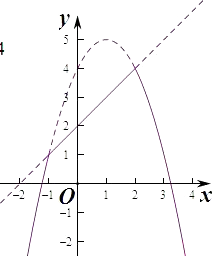
【考點精析】本題主要考查了函數的最值及其幾何意義的相關知識點,需要掌握利用二次函數的性質(配方法)求函數的最大(小)值;利用圖象求函數的最大(小)值;利用函數單調性的判斷函數的最大(小)值才能正確解答此題.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案 新思維寒假作業系列答案
新思維寒假作業系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓E的中心在坐標原點,左、右焦點F1、F2分別在x軸上,離心率為 ![]() ,在其上有一動點A,A到點F1距離的最小值是1,過A、F1作一個平行四邊形,頂點A、B、C、D都在橢圓E上,如圖所示.
,在其上有一動點A,A到點F1距離的最小值是1,過A、F1作一個平行四邊形,頂點A、B、C、D都在橢圓E上,如圖所示.
(Ⅰ)求橢圓E的方程;
(Ⅱ)判斷ABCD能否為菱形,并說明理由.
(Ⅲ)當ABCD的面積取到最大值時,判斷ABCD的形狀,并求出其最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直四棱柱ABCD﹣A1B1C1D1底面是邊長為1的正方形,高AA1= ![]() ,點A是平面α內的一個定點,AA1與α所成角為
,點A是平面α內的一個定點,AA1與α所成角為 ![]() ,點C1在平面α內的射影為P,當四棱柱ABCD﹣A1B1C1D1按要求運動時(允許四棱柱上的點在平面α的同側或異側),點P所經過的區域的面積= .
,點C1在平面α內的射影為P,當四棱柱ABCD﹣A1B1C1D1按要求運動時(允許四棱柱上的點在平面α的同側或異側),點P所經過的區域的面積= . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了了解某地區電視觀眾對某類體育節目的收視情況隨機抽取了100名觀眾進行調查,其中女性有55名.如圖是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖.將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”,已知“體育迷”中有10名女性.
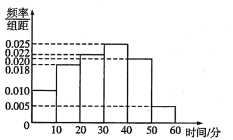
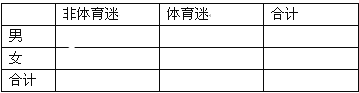
(1)根據已知條件完成下面的![]() 列聯表,并據此資料你是否認為“體育迷”與性別有關?
列聯表,并據此資料你是否認為“體育迷”與性別有關?
(2)將日均收看該體育節目不低于50分鐘的觀眾稱為“超級體育迷”,已知“超級體育迷”中有2名女性,若從“超級體育迷”中任意選取2人,求至少有1名女性觀眾的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的各項都大于1,且a1=2,a ![]() ﹣an+1﹣a
﹣an+1﹣a ![]() +1=0(n∈N*).
+1=0(n∈N*).
(1)求證: ![]() ≤an<an+1≤n+2;
≤an<an+1≤n+2;
(2)求證: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <1.
<1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域
的定義域![]() ,值域是
,值域是![]() ;
;![]() 定義域
定義域![]() ,值域是
,值域是![]() ,其中實數
,其中實數![]() 滿足
滿足![]() .
.
甲:如果任意![]() ,存在
,存在![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
乙:如果存在![]() ,存在
,存在![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
丙:如果任意![]() ,任意
,任意![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
丁:如果存在![]() ,任意
,任意![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
請判斷上述四個命題中,假命題的個數是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知存在常數![]() ,那么函數
,那么函數![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數,再由函數的奇偶性可知在
上是增函數,再由函數的奇偶性可知在![]() 上是增函數,在
上是增函數,在![]() 上是減函數.
上是減函數.
(1)判斷函數![]() 的單調性,并證明:
的單調性,并證明:
(2)將前述的函數![]() 和
和![]() 推廣為更為一般形式的函數
推廣為更為一般形式的函數![]() ,使
,使![]() 和
和![]() 都是
都是![]() 的特例,研究
的特例,研究![]() 的單調性(只須歸納出結論,不必推理證明)
的單調性(只須歸納出結論,不必推理證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)上的點到它的兩個焦點的距離之和為4,以橢圓C的短軸為直徑的圓O經過兩個焦點,A,B是橢圓C的長軸端點.
=1(a>b>0)上的點到它的兩個焦點的距離之和為4,以橢圓C的短軸為直徑的圓O經過兩個焦點,A,B是橢圓C的長軸端點. 
(1)求橢圓C的標準方程和圓O的方程;
(2)設P、Q分別是橢圓C和圓O上位于y軸兩側的動點,若直線PQ與x平行,直線AP、BP與y軸的交點即為M、N,試證明∠MQN為直角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中錯誤的是( )
A. 給定兩個命題![]() ,若
,若![]() 為真命題,則
為真命題,則![]() 都是假命題;
都是假命題;
B. 命題“若![]() ,則
,則![]() ”的逆否命題是“若
”的逆否命題是“若![]() ,則
,則![]() ”;
”;
C. 若命題![]() ,則
,則![]() ,使得
,使得![]() ;
;
D. 函數![]() 在
在![]() 處的導數存在,若
處的導數存在,若![]() 是
是![]() 的極值點,則
的極值點,則![]() 是
是![]() 的充要條件.
的充要條件.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com