【題目】從某居民區隨機抽取10個家庭，獲得第i個家庭的月收入xi(單位：千元)與月儲蓄yi(單位：千元)的數據資料，算得 ＝80， ＝20， i＝184， ＝720.
(1)求家庭的月儲蓄y對月收入x的線性回歸方程
；
(2)判斷變量x與y之間是正相關還是負相關；
(3)若該居民區某家庭月收入為7千元，預測該家庭的月儲蓄．
附：線性回歸方程
中， 
，其中
為樣本平均值．
【答案】（1）
＝0.3x－0.4.（2）正相關（3）1.7
【解析】試題分析：1）由題意可知n， 
，進而代入可得b、a值，可得方程；
（2）由回歸方程x的系數b的正負可判；
（3）把x=7代入回歸方程求其函數值即可．
試題解析：
解：(1)由題意知n＝10，
＝
i＝
＝8，
＝ 
i＝
＝2，
又－n
2＝720－10×82＝80，
iyi－n＝184－10×8×2＝24，
由此得
＝
＝0.3，
＝－＝2－0.3×8＝－0.4，
故所求線性回歸方程為
＝0.3x－0.4.
(2)由于變量y的值隨x值的增加而增加(＝0.3>0)，故x與y之間是正相關．
(3)將x＝7代入回歸方程可以預測該家庭的月儲蓄為＝0.3×7－0.4＝1.7(千元)．
科目：高中數學 來源： 題型：
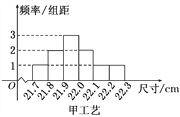
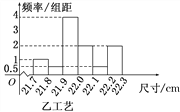
【題目】某工廠用甲、乙兩種不同工藝生產一大批同一種零件，零件尺寸均在[21.7，22.3](單位：cm)之間，把零件尺寸在[21.9,22.1)的記為一等品，尺寸在[21.8,21.9)∪[22.1,22.2)的記為二等品，尺寸在[21.7，21.8)∪[22.2，22.3]的記為三等品，現從甲、乙工藝生產的零件中各隨機抽取100件產品，所得零件尺寸的頻率分布直方圖如圖所示．
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
附：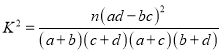 
(1)根據上述數據完成下列2×2列聯表，根據此數據，你認為選擇不同的工藝與生產出一等品是否有關？
甲工藝 | 乙工藝 | 總計 | |
一等品 | |||
非一等品 | |||
總計 |
(2)以上述各種產品的頻率作為各種產品發生的概率，若一等品、二等品、三等品的單件利潤分別為30元、20元、15元，你認為以后該工廠應該選擇哪種工藝生產該種零件？請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知(2x－3y)9＝a0x9＋a1x8y＋a2x7y2＋…＋a9y9，求：
(1)各項系數之和；
(2)所有奇數項系數之和；
(3)系數絕對值的和；
(4)分別求出奇數項的二項式系數之和與偶數項的二項式系數之和．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
.
（1）函數
在區間
是單調函數，求實數
的取值范圍；
（2）若存在
，使得
成立，求滿足條件的最大整數
；
（3）如果對任意的
都有
成立，求實數的范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠為了對新研發的一種產品進行合理定價，將該產品按事先擬定的價格進行試銷，得到如下數據：
單價x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
單價x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回歸直線方程
，其中
， 
；
(2)預計在今后的銷售中，銷量與單價仍然服從(1)中的關系，且該產品的成本是4元/件，為使工廠獲得最大利潤，該產品的單價應定為多少元？(利潤＝銷售收入－成本)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】8人排成一排照相，分別求下列條件下的不同照相方式的種數.
（1）其中甲、乙相鄰，丙、丁相鄰；
（2）其中甲、乙不相鄰，丙、丁不相鄰；
（要求寫出解答過程，并用數字作答）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）△ABC中，角A，B，C所對的邊分別為a，b，c．已知a＝3，cos A＝
，B＝A＋
．
（1）求b的值；
（2）求△ABC的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】判斷下列命題的真假，并說明理由．
(1)x∈R，都有x2－x＋1>
；
(2)α，β，使cos(α－β)＝cos α－cos β；
(3)x，y∈N，都有(x－y)∈N；
(4)x，y∈Z，使
x＋y＝3.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
