
【題目】函數![]()
(1)當![]() 時,求函數
時,求函數![]() 的定義域;
的定義域;
(2)若![]()
![]() ,請判定
,請判定![]() 的奇偶性;
的奇偶性;
(3)是否存在實數![]() ,使函數
,使函數![]() 在
在![]() 遞增,并且最大值為1,若存在,求出
遞增,并且最大值為1,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)定義域為![]() ;(2)奇函數;(3)存在,
;(2)奇函數;(3)存在,![]() .
.
【解析】
試題分析:(1)當![]() 時,函數
時,函數![]() 的定義域為
的定義域為![]() ,
,![]() ;(2)
;(2)![]() ,函數
,函數![]() 的定義域為
的定義域為![]() ,即
,即![]() ,關于原點對稱,又
,關于原點對稱,又![]() ,所以函數
,所以函數![]() 為奇函數;(3)假設存在,設
為奇函數;(3)假設存在,設![]() ,由于
,由于![]() ,所以
,所以![]() 在區間
在區間![]() 上單調遞減,若底數
上單調遞減,若底數![]() ,根據復合函數單調性可知,函數
,根據復合函數單調性可知,函數![]() 在區間
在區間![]() 上單調遞減,不符合題意,若底數
上單調遞減,不符合題意,若底數![]() ,根據復合函數單調性可知,函數
,根據復合函數單調性可知,函數![]() 在區間
在區間![]() 上單調遞增,所以當
上單調遞增,所以當![]() 時,取得最大值1,即
時,取得最大值1,即![]() ,
,![]() ,所以
,所以![]() ,符合題意.
,符合題意.
試題解析:(1)由題意:![]() ,
,![]() ,即
,即![]() ,
,
所以函數![]() 的定義域為
的定義域為![]() .
.
(2)易知![]()
![]() ,
,
∵![]() ,且
,且![]() ,∴
,∴![]() ,關于原點對稱,
,關于原點對稱,
又∵![]()
![]() =
=![]() ,
,
∴![]()
![]() =-
=-![]() =-
=-![]() ,
,
∴![]() 為奇函數.
為奇函數.
(3)令![]() ,
, ![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,
又∵函數![]() 在
在![]() 遞增, ∴
遞增, ∴![]() ,
,
又![]() 函數
函數![]() 在
在![]() 的最大值為1,
的最大值為1,![]() ,
,
即![]() ,
,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知點![]() ,圓
,圓![]() 是以
是以![]() 的中點為圓心,
的中點為圓心, ![]() 為半徑的圓.
為半徑的圓.
(Ⅰ)若圓![]() 的切線在
的切線在![]() 軸和
軸和![]() 軸上截距相等,求切線方程;
軸上截距相等,求切線方程;
(Ⅱ)若![]() 是圓
是圓![]() 外一點,從
外一點,從![]() 向圓
向圓![]() 引切線
引切線![]() ,
, ![]() 為切點,
為切點, ![]() 為坐標原點,且有
為坐標原點,且有![]() ,求使
,求使![]() 最小的點
最小的點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,
,![]() ,
,![]() 為常數
為常數
(1)用![]() 表示
表示![]() 的最小值,求
的最小值,求![]() 的解析式
的解析式
(2)在(1)中,是否存在最小的整數![]() ,使得
,使得![]() 對于任意
對于任意![]() 均成立,若存在,求出
均成立,若存在,求出![]() 的值;若不存在,請說明理由
的值;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
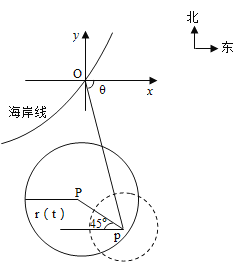
【題目】在某海濱城市附近海面有一臺風,據監測,當前臺風中心位于城市![]() (如圖)的東偏南
(如圖)的東偏南![]() 方向300km的海面
方向300km的海面![]() 處,并以20km/h的速度向西偏北
處,并以20km/h的速度向西偏北![]() 方向移動,臺風侵襲的范圍為圓形區域,當前半徑為60km,并以10km/h的速度不斷增大,問幾小時后該城市開始受到臺風的侵襲?受到臺風侵襲的時間有多少小時?
方向移動,臺風侵襲的范圍為圓形區域,當前半徑為60km,并以10km/h的速度不斷增大,問幾小時后該城市開始受到臺風的侵襲?受到臺風侵襲的時間有多少小時?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A,B,若A不是B的子集,則下列命題中正確的是( )
A.對任意的a∈A,都有aB
B.對任意的b∈B,都有bA
C.存在a0 , 滿足a0∈A,a0B
D.存在a0 , 滿足a0∈A,a0∈B
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)某旅行社設計了一個組織旅游團包飛機去廣州旅游的方案,其中旅行杜的包機費用為![]() 元,旅游團中最多能有
元,旅游團中最多能有![]() 人,并且旅游團中的人數
人,并且旅游團中的人數![]() (單位:個)與每個人交給旅行社的費用
(單位:個)與每個人交給旅行社的費用![]() (單位:元)的關系如下:
(單位:元)的關系如下: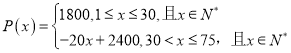 .
.
(1)將旅行社的利潤![]() (單位:元)表示成旅游團中的人數
(單位:元)表示成旅游團中的人數![]() 的函數(注:利潤=收取的費用一包機費用);
的函數(注:利潤=收取的費用一包機費用);
(2)當旅游團有多少人時,旅行社的利潤最大?并求出最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com