解:(Ⅰ)依題意,直線l顯然不平行于坐標軸,
故y=k(x+1)可化為
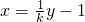
將
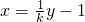
代入x
2+3y
2=a
2,消去x,
得
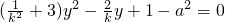
①
由直線l與橢圓相交于兩個不同的點,得
△=
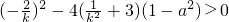
化簡整理即得
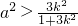
.(☆)
(Ⅱ)A(x
1,y
1),B(x
2,y
2),
由①,得
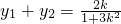
②
因為
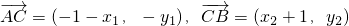
,由
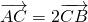
,
得y
1=-2y
2③
由②③聯立,解得y
2=
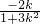
④
△OAB的面積
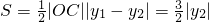
=
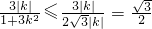
上式取等號的條件是3k
2=1,即
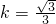
當
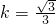
時,由④解得
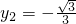
;
當
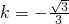
時,由④解得
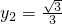
.
將
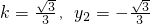
及
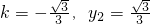
這兩組值分別代入①,
均可解出a
2=5
經驗證,a
2=5,
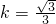
滿足(☆)式.
所以,△OAB的面積取得最大值時橢圓方程是x
2+3y
2=5
注:若未驗證(說明
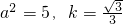
)滿足(☆)式,.
分析:(I)設直線l的方程為y=k(x+1),將直線的方程代入拋物線的方程,消去x得到關于y的一元二次方程,再結合直線l與橢圓相交于兩個不同的點得到根的判別式大于0,從而解決問題.
(II)設A(x
1,y
1),B(x
2,y
2),由(I),得
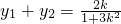
,由
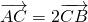
,得y
2=
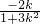
從而求得△OAB的面積,最后利用基本不等式求得其最大值,及取值最大值時的k值,從而△OAB的面積取得最大值時橢圓方程即可.
點評:本小題主要考查直線與圓錐曲線的綜合問題、基本不等式、橢圓方程等基礎知識,考查運算求解能力、化歸與轉化思想.屬于中檔題.

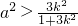 ;
;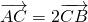 ,△OAB的面積取得最大值時橢圓方程.
,△OAB的面積取得最大值時橢圓方程.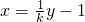
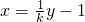 代入x2+3y2=a2,消去x,
代入x2+3y2=a2,消去x,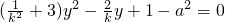 ①
①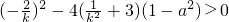
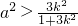 .(☆)
.(☆)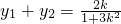 ②
②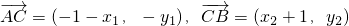 ,由
,由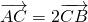 ,
,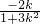 ④
④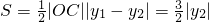
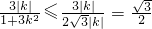
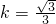
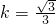 時,由④解得
時,由④解得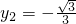 ;
;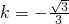 時,由④解得
時,由④解得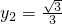 .
.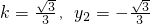 及
及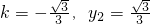 這兩組值分別代入①,
這兩組值分別代入①,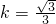 滿足(☆)式.
滿足(☆)式.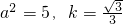 )滿足(☆)式,.
)滿足(☆)式,.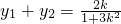 ,由
,由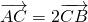 ,得y2=
,得y2=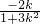 從而求得△OAB的面積,最后利用基本不等式求得其最大值,及取值最大值時的k值,從而△OAB的面積取得最大值時橢圓方程即可.
從而求得△OAB的面積,最后利用基本不等式求得其最大值,及取值最大值時的k值,從而△OAB的面積取得最大值時橢圓方程即可.

 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案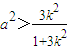 ;
;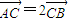 ,△OAB的面積取得最大值時橢圓方程.
,△OAB的面積取得最大值時橢圓方程.