Question

求曲線f（x）=x³-3x²+2x過原點的切線方程．

Answer 1

解f′（x）=3x²-6x+2．設切線的斜率為k．
（1）當切點是原點時k=f′（0）=2，
所以所求曲線的切線方程為y=2x．
（2）當切點不是原點時，設切點是（x₀，y₀），
則有y₀=x₀³-3x₀²+2x₀，k=f′（x₀）=3x₀²-6x₀+2，①
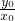
又k==x₀²-3x₀+2，②
由①②得x₀=，k==-．
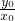
∴所求曲線的切線方程為y=-x．
故曲線的切線方程是y=2x；y=-
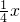
分析：求出函數的導數，利用導數的幾何意義：切點處的導數值是切線的斜率，分原點是切點和原點不是切點兩類求．
點評：本題考查導數的幾何意義：切點處的導數值是切線的斜率；注意“在點處的切線”與“過點的切線”的區別．