【答案】
分析:(Ⅰ)因為每個數位上都是0或者1,取差的絕對值仍然是0或者1,符合S
n的要求.
然后是減去C的數位,不管減去的是0還是1,每一個a和每一個b都是同時減去的,
因此不影響他們原先的差.
(Ⅱ)先比較A和B有幾個不同(因為距離就是不同的有幾個),然后比較A和C有幾個不同,
這兩者重復的(就是某一位上A和B不同,A和C不同,那么這一位上B和C就相同)去掉兩次
(因為在前兩次比較中各計算了一次),剩下的就是B和C的不同數目,
很容易得到這樣的關系式:h=k+l-2i,從而三者不可能同為奇數.
(Ⅲ)首先理解P中會出現C
m2個距離,所以平均距離就是距離總和再除以C
m2,
而距離的總和仍然可以分解到每個數位上,第一位一共產生了多少個不同,
第二位一共產生了多少個不同,如此下去,直到第n位.然后思考,
第一位一共m個數,只有0和1會產生一個單位距離,因此只要分開0和1的數目即可,
等算出來
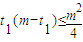
,一切就水到渠成了.
此外,這個問題需要注意一下數學語言的書寫規范.
解答:解:(1)設A=(a
1,a
2,…,a
n),B=(b
1,b
2,…,b
n),C=(c
1,c
2,..,c
n)∈S
n因a
i,b
i∈0,1,故|a
i-b
i|∈0,1,(i=1,2,…,n)a
1b
1∈0,1,
即A-B=(|a
1-b
1|,|a
2-b
2|,…,|a
n-b
n|)∈S
n又a
i,b
i,c
i∈(0,1),i=1,2,…,n
當c
i=0時,有||a
i-c
i|-|b
i-c
i||=|a
i-b
i|;
當c
i=1時,有||a
i-c
i|-|b
i-c
i||=|(1-a
i)-(1-b
i)=|a
i-b
i|
故
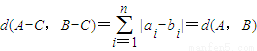
(2)設A=(a
1,a
2,…,a
n),B=(b
1,b
2,…,b
n),C=(c
1,c
2,..,c
n)∈S
n記d(A,B)=k,d(A,C)=l,d(B,C)=h
記O=(0,0,…,0)∈S
n,由第一問可知:
d(A,B)=d(A-A,B-A),d=(O,B-A)=k
d(A,C)=d(A-A,C-A)=d(O,C-A)=l
d(B,C)=d(B-A,C-A)=h
即|b
i-a
i|中1的個數為k,|c
i-a
i|中1的個數為l,(i=1,2,…,n)
設t是使|b
i-a
i|=|c
i-a
i|=1成立的i的個數,則有h=k+l-2t,
由此可知,k,l,h不可能全為奇數,即d(A,B),d(A,C),d(B,C)三個數中至少有一個是偶數.
(3)顯然P中會產生C
m2個距離,也就是說
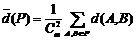
,其中
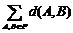
表示P中每兩個元素距離的總和.
分別考察第i個位置,不妨設P中第i個位置一共出現了t
i個1,那么自然有m-t
i個0,因此在這個位置上所產生的距離總和為
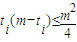
,(i=1,2,…,n),
那么n個位置的總和
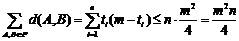
即
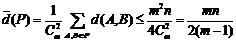 點評:
點評:本題是綜合考查集合、數列與推理綜合的應用,這道題目的難點主要出現在讀題上,需要仔細分析,以找出解題的突破點.題目所給的條件其實包含兩個定義,第一個是關于S
n的,其實S
n中的元素就是一個n維的坐標,其中每個坐標值都是0或者1,也可以這樣理解,就是一個n位數字的數組,每個數字都只能是0和1,第二個定義叫距離,距離定義在兩者之間,如果直觀理解就是看兩個數組有多少位不同,因為只有0和1才能產生一個單位的距離,因此這個大題最核心的就是處理數組上的每一位數,然后將處理的結果綜合起來,就能看到整體的性質了.

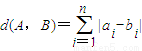
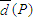 .
.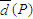 ≤
≤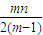 .
.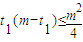 ,一切就水到渠成了.
,一切就水到渠成了.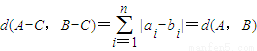
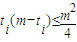 ,(i=1,2,…,n),
,(i=1,2,…,n),





