
分析 根據題意確定函數的解析式為f(x)=$\left\{\begin{array}{l}{2{x}^{2}-2x,x≤1}\\{1-{x}^{2},x>1}\end{array}\right.$,畫出函數的圖象從圖象上觀察當關于x的方程為f(x)=m(m∈R)恰有三個互不相等的實數根時m的取值范圍.
解答 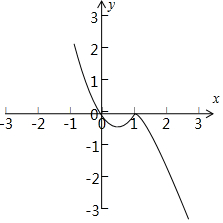 解:由 2x≤x+1 可得 x≤1,由 2x>x+1 可得 x>1.
解:由 2x≤x+1 可得 x≤1,由 2x>x+1 可得 x>1.
∴根據題意得f(x)=$\left\{\begin{array}{l}{2{x}^{2}-2x,x≤1}\\{1-{x}^{2},x>1}\end{array}\right.$,
根據函數的極大值為f($\frac{1}{2}$)=-$\frac{1}{4}$,關于x的方程f(x)=m(m∈R)恰有三個互相等的實數根,
可得m的取值范圍是(-$\frac{1}{4}$,0),
故答案為(-$\frac{1}{4}$,0).
點評 本題主要考查函數的零點的定義,函數的零點與方程的根的關系,體現了轉化、數形結合的數學思想,屬于中檔題.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,3] | B. | [-1,1] | C. | (-1,1) | D. | [1,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=-x+1 | B. | y=|x| | C. | $y=\frac{1}{x}$ | D. | $y=\frac{1}{{{x^2}+1}}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
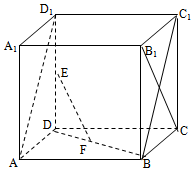 如圖,在棱長為2的正方體ABCD-A1B1C1D1中,E、F分別為DD1、BD的中點.
如圖,在棱長為2的正方體ABCD-A1B1C1D1中,E、F分別為DD1、BD的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com