【題目】若直線 l1和l2 是異面直線，l1在平面 α內，l2在平面β內，l是平面α與平面β的交線，則下列命題正確的是（ ）
A.l與l1 ， l2都不相交
B.l與l1 ， l2都相交
C.l至多與l1 ， l2中的一條相交
D.l至少與l1 ， l2中的一條相交
【答案】D
【解析】解：A．l與l1 ， l2可以相交，如圖： 
∴該選項錯誤；
B．l可以和l1 ， l2中的一個平行，如上圖，∴該選項錯誤；
C．l可以和l1 ， l2都相交，如下圖：
，∴該選項錯誤；
D．“l至少與l1 ， l2中的一條相交”正確，假如l和l1 ， l2都不相交；
∵l和l1 ， l2都共面；
∴l和l1 ， l2都平行；
∴l1∥l2 ， l1和l2共面，這樣便不符合已知的l1和l2異面；
∴該選項正確．
故選D．
可以畫出圖形來說明l與l1 ， l2的位置關系，從而可判斷出A，B，C是錯誤的，而對于D，可假設不正確，這樣l便和l1 ， l2都不相交，這樣可推出和l1 ， l2異面矛盾，這樣便說明D正確．
全能測控期末小狀元系列答案科目：高中數學 來源： 題型：
【題目】下列命題：
①命題“x∈R，x2+x+1=0”的否定是“x∈R，x2+x+1≠0”；
②若A={x|x＞0}，B={x|x≤﹣1}，則A∩（RB）=A；
③函數f（x）=sin（ωx+φ）（ω＞0）是偶函數的充要條件是φ=kπ+ 
（k∈Z）；
④若非零向量 
， 
滿足 =λ ， =λ （λ∈R），則λ=1．
其中正確命題的序號有
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學一位高三班主任對本班50名學生學習積極性和對待班級工作的態度進行調查，得到的統計數據如表所示：
積極參加班級工作 | 不積極參加班級工作 | 合計 | |
學習積極性高 | 18 | 7 | 25 |
學習積極性不高 | 6 | 19 | 25 |
合計 | 24 | 26 | 50 |
（1）如果隨機調查這個班的一名學生，那么抽到不積極參加班級工作且學習積極性不高的學生的概率是多少？
（2）若不積極參加班級工作且學習積極性高的7名學生中有兩名男生，現從中抽取2名學生參加某項活動，問2名學生中有1名男生的概率是多少？
（3）學生的學習積極性與對待班級工作的態度是否有關系？請說明理由．
附：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a≠0，集合A={x|x2﹣x﹣6＜0}，B={x|x2+2x﹣8≥0}，C={x|x2﹣4ax+3a2＜0}，且C（A∩RB）．求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業為了對新研發的一批產品進行合理定價，將產品按事先擬定的價格進行試銷，得到一組銷售數據
，如表所示：
已知
（1）求
的值
（2）已知變量
具有線性相關性，求產品銷量
關于試銷單價
的線性回歸方程
可供選擇的數據
（3）用
表示（2）中所求的線性回歸方程得到的與
對應的產品銷量的估計值。當銷售數據
對應的殘差的絕對值
時，則將銷售數據
稱為一個“好數據”。試求這6組銷售數據中的 “好數據”。
參考數據：線性回歸方程中
的最小二乘估計分別是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱錐P﹣ABC中，△ABC是等邊三角形，D是AC的中點，PA=PC，二面角P﹣AC﹣B的大小為60°；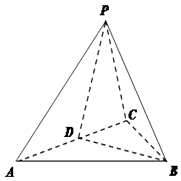 
（1）求證：平面PBD⊥平面PAC；
（2）求AB與平面PAC所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】乒乓球單打比賽在甲、乙兩名運動員間進行，比賽采用7局4勝制（即先勝4局者獲勝，比賽結束），假設兩人在每一局比賽中獲勝的可能性相同．
（1）求甲以4比1獲勝的概率；
（2）求乙獲勝且比賽局數多于5局的概率；
（3）求比賽局數的分布列．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
