
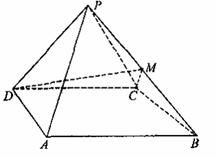
如圖,四棱錐![]() 中,側(cè)面
中,側(cè)面![]() 是邊長為2的正三角形,且與底面垂直,底面
是邊長為2的正三角形,且與底面垂直,底面![]() 是
是![]() 的菱形,
的菱形,![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
(Ⅰ)求![]() 與底面
與底面![]() 所成角的大小;
所成角的大小;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
解析:求線面角關(guān)鍵是作垂線,找射影,求異面直線所成的角采用平
移法![]() 求二面角的大小也可應(yīng)用面積射影法,比較好的方法是向量法
求二面角的大小也可應(yīng)用面積射影法,比較好的方法是向量法![]()
答案:(I)取DC的中點(diǎn)O,由ΔPDC是正三角形,有PO⊥DC.
又∵平面PDC⊥底面ABCD,∴PO⊥平面ABCD于O.
連結(jié)OA,則OA是PA在底面上的射影.∴∠PAO就是PA與底面所成角.
∵∠ADC=60°,由已知ΔPCD和ΔACD是全等的正三角形,從而求得OA=OP=![]() .
.
∴∠PAO=45°.∴PA與底面ABCD可成角的大小為45°. ……6分
(II)由底面ABCD為菱形且∠ADC=60°,DC=2,DO=1,有OA⊥DC.
建立空間直角坐標(biāo)系如圖,則![]() ,
, ![]() .
.
 由M為PB中點(diǎn),∴
由M為PB中點(diǎn),∴![]() .
.
∴![]()
![]() .
.
∴![]() ,
,
![]() .
.
∴PA⊥DM,PA⊥DC. ∴PA⊥平面DMC. ……4分
(III)![]() .令平面BMC的法向量
.令平面BMC的法向量![]() ,
,
則![]() ,從而x+z=0; ……①,
,從而x+z=0; ……①, ![]() ,從而
,從而![]() . ……②
. ……②
由①、②,取x=−1,則![]() . ∴可取
. ∴可取![]() .
.
由(II)知平面CDM的法向量可取![]() ,
,
∴![]() . ∴所求二面角的余弦值為-
. ∴所求二面角的余弦值為-![]() . ……6分
. ……6分
法二:(Ⅰ)方法同上
(Ⅱ)取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() ,由(Ⅰ)知,在菱形
,由(Ⅰ)知,在菱形![]() 中,由于
中,由于![]() ,
,
則![]() ,又
,又![]() ,則
,則![]() ,即
,即![]() ,
,
又在![]() 中,中位線
中,中位線![]()
![]() ,
,![]() ,則
,則![]() ,
,
則四邊形![]() 為
為![]() ,所以
,所以![]() ,在
,在![]() 中,
中,![]() ,
,
則![]() ,故
,故![]() 而
而![]() ,
,
則![]()
(Ⅲ)由(Ⅱ)知![]() ,則
,則![]() 為二面角
為二面角![]() 的平面角,
的平面角,
在![]()
![]() 中,易得
中,易得![]()
![]() ,
,![]() ,
,
![]() 故,所求二面角的余弦值為
故,所求二面角的余弦值為![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
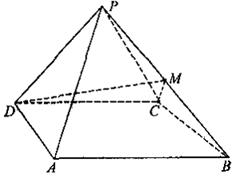
如圖,四棱錐![]() 中,側(cè)面
中,側(cè)面![]() 是邊長為2的正三角形,且與底面垂直,底面
是邊長為2的正三角形,且與底面垂直,底面![]() 是
是![]() 的菱形,
的菱形,![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
(Ⅰ) 求證:![]() 平面
平面![]() ;
;
(Ⅱ) 求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011屆河北省邯鄲一中高三高考?jí)狠S模擬考試文數(shù) 題型:解答題
(本小題12分)如圖,四棱錐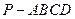 中,
中,
側(cè)面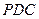 是邊長為2的正三角形,且與底面垂直,底面
是邊長為2的正三角形,且與底面垂直,底面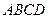 是
是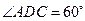 的菱形,
的菱形,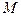 為
為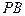 的中點(diǎn).
的中點(diǎn).
(1)求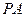 與底面
與底面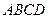 所成角的大小;
所成角的大小;
(2)求證: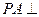 平面
平面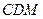 ;
;
(3)求二面角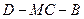 的余弦值.
的余弦值. 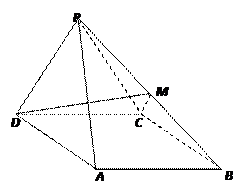
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年福建省高三12月月考理科數(shù)學(xué)試卷(解析版) 題型:解答題
如圖,四棱錐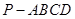 中,側(cè)面
中,側(cè)面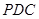 是邊長為2的正三角形,且與底面垂直,底面
是邊長為2的正三角形,且與底面垂直,底面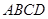 是
是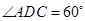 的菱形,
的菱形,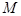 為
為 的中點(diǎn).
的中點(diǎn).
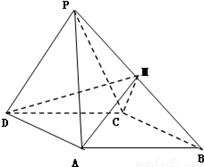
(Ⅰ)求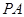 與底面
與底面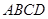 所成角的大小;
所成角的大小;
(Ⅱ)求證: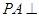 平面
平面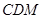 ;(Ⅲ)求二面角
;(Ⅲ)求二面角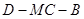 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年河北省高三高考?jí)狠S模擬考試文數(shù) 題型:解答題
(本小題12分)如圖,四棱錐 中,
中,
側(cè)面 是邊長為2的正三角形,且與底面垂直,底面
是邊長為2的正三角形,且與底面垂直,底面 是
是 的菱形,
的菱形, 為
為 的中點(diǎn).
的中點(diǎn).
(1)求 與底面
與底面 所成角的大小;
所成角的大小;
(2)求證: 平面
平面 ;
;
(3)求二面角 的余弦值.
的余弦值.

查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com