
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,且對任意的正整數(shù)
,且對任意的正整數(shù)![]() ,都有
,都有![]() ,其中常數(shù)
,其中常數(shù)![]() .設
.設![]()
![]() ﹒
﹒
(1)若![]() ,求數(shù)列
,求數(shù)列![]() 的通項公式;
的通項公式;
(2)若![]() 且
且![]() ,設
,設![]()
![]() ,證明數(shù)列
,證明數(shù)列![]() 是等比數(shù)列;
是等比數(shù)列;
(3)若對任意的正整數(shù)![]() ,都有
,都有![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)詳見解析(3)
(2)詳見解析(3)![]()
【解析】
試題(1)先根據(jù)和項與通項關系,將條件![]() 轉(zhuǎn)化為
轉(zhuǎn)化為![]() ,即
,即![]() ,再根據(jù)題設條件進行構(gòu)造數(shù)列
,再根據(jù)題設條件進行構(gòu)造數(shù)列![]() :
:![]() ,即
,即![]() ,最后根據(jù)等差數(shù)列定義得證(2)先根據(jù)等比數(shù)列定義明確目標:
,最后根據(jù)等差數(shù)列定義得證(2)先根據(jù)等比數(shù)列定義明確目標: 為一個常數(shù),因此利用
為一個常數(shù),因此利用![]() ,代入化簡得為
,代入化簡得為![]() ,因此
,因此![]() 是首項為
是首項為![]() ,公比為
,公比為![]() 的等比數(shù)列,(3)先化簡不等式
的等比數(shù)列,(3)先化簡不等式![]() ,實質(zhì)討論數(shù)列
,實質(zhì)討論數(shù)列![]() :當
:當![]() 時,
時,![]() ,當
,當![]() 且
且![]() 時,
時,![]() .若
.若![]() ,則
,則![]() ,然后分別解不等式
,然后分別解不等式![]() ,難點在當
,難點在當![]() 且
且![]() 時,需分類討論:若
時,需分類討論:若![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,![]() ,不符合,舍去.若
,不符合,舍去.若![]() 時,
時,![]() ,
,![]() ,
,![]() ,只須
,只須![]() 即可,顯然成立.故
即可,顯然成立.故![]() 符合條件;若
符合條件;若![]() 時,
時,![]() ,
,![]() ,從而
,從而![]() ,故
,故![]() ,只須
,只須![]() 即可,于是
即可,于是![]() .
.
試題解析:解:∵![]() ,
,![]() ,
,
∴當![]() 時,
時,![]() ,
,
從而![]() ,
,![]() ,
,![]() ﹒
﹒
又在![]() 中,令
中,令![]() ,可得
,可得![]() ,滿足上式,
,滿足上式,
所以![]() ,
,![]() ﹒
﹒
(1)當![]() 時,
時,![]() ,
,![]() ,
,
從而![]() ,即
,即![]() ,
,
又![]() ,所以數(shù)列
,所以數(shù)列![]() 是首項為1,公差為
是首項為1,公差為![]() 的等差數(shù)列,
的等差數(shù)列,
所以![]() .
.
(2)當![]() 且
且![]() 且
且![]() 時,
時,
![]()
![]() ,
,
又![]() ,
,
所以![]() 是首項為
是首項為![]() ,公比為
,公比為![]() 的等比數(shù)列,
的等比數(shù)列,![]() ﹒
﹒
(3)在(2)中,若![]() ,則
,則![]() 也適合,所以當
也適合,所以當![]() 時,
時,![]() .
.
從而由(1)和(2)可知
當![]() 時,
時,![]() ,顯然不滿足條件,故
,顯然不滿足條件,故![]() .
.
當![]() 時,
時,![]() .
.
若![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,![]() ,不符合,舍去.
,不符合,舍去.
若![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
所以只須![]() 即可,顯然成立.故
即可,顯然成立.故![]() 符合條件;
符合條件;
若![]() 時,
時,![]() ,滿足條件.故
,滿足條件.故![]() 符合條件;
符合條件;
若![]() 時,
時,![]() ,
,![]() ,從而
,從而![]() ,
,![]() ,
,
因為![]() .故
.故![]() , 要使
, 要使![]() 成立,只須
成立,只須![]() 即可.
即可.
于是![]() .
.
綜上所述,所求實數(shù)![]() 的范圍是
的范圍是![]() .
.


 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知正方體![]() 的棱長為
的棱長為![]() ,點
,點![]() 分別為棱
分別為棱![]() 的中點,下列結(jié)論中,其中正確的個數(shù)是( )
的中點,下列結(jié)論中,其中正確的個數(shù)是( )
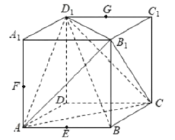
①過![]() 三點作正方體的截面,所得截面為正六邊形;
三點作正方體的截面,所得截面為正六邊形;
②![]() /平面
/平面![]() ;
;
③![]() ;
;
④異面直線![]() 與
與![]() 所成角的正切值為
所成角的正切值為![]() ;
;
⑤四面體![]() 的體積等于
的體積等于![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù))。曲線
為參數(shù))。曲線![]() 的參數(shù)方程為
的參數(shù)方程為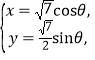 (
(![]() 為參數(shù)),在以坐標原點為極點,
為參數(shù)),在以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求曲線![]() ,
,![]() 的極坐標方程;
的極坐標方程;
(2)在極坐標系中,射線![]() 與曲線
與曲線![]() 交于點
交于點![]() ,射線
,射線![]() 與曲線
與曲線![]() 交于點
交于點![]() ,求
,求![]() 的面積(其中
的面積(其中![]() 為坐標原點).
為坐標原點).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知![]() 是一幢6層的寫字樓,每層高均為3m,在
是一幢6層的寫字樓,每層高均為3m,在![]() 正前方36m處有一建筑物
正前方36m處有一建筑物![]() ,從樓頂
,從樓頂![]() 處測得建筑物
處測得建筑物![]() 的張角為
的張角為![]() .
.
(1)求建筑物![]() 的高度;
的高度;
(2)一攝影愛好者欲在寫字樓![]() 的某層拍攝建筑物
的某層拍攝建筑物![]() .已知從攝影位置看景物所成張角最大時,拍攝效果最佳.問:該攝影愛好者在第幾層拍攝可取得最佳效果(不計人的高度)?
.已知從攝影位置看景物所成張角最大時,拍攝效果最佳.問:該攝影愛好者在第幾層拍攝可取得最佳效果(不計人的高度)?

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某測試團隊為了研究“飲酒”對“駕車安全”的影響,隨機選取100名駕駛員先后在無酒狀態(tài)、酒后狀態(tài)下進行“停車距離”測試.測試的方案:電腦模擬駕駛,以某速度勻速行駛,記錄下駕駛員的“停車距離”(駕駛員從看到意外情況到車子完全停下所需要的距離).無酒狀態(tài)與酒后狀態(tài)下的試驗數(shù)據(jù)分別列于表1和表2.
表1
停車距離 |
|
|
|
|
|
頻數(shù) | 26 |
|
| 8 | 2 |
表2
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 |
平均停車距離 | 30 | 50 | 60 | 70 | 90 |
已知表1數(shù)據(jù)的中位數(shù)估計值為26,回答以下問題.
(Ⅰ)求![]() 的值,并估計駕駛員無酒狀態(tài)下停車距離的平均數(shù);
的值,并估計駕駛員無酒狀態(tài)下停車距離的平均數(shù);
(Ⅱ)根據(jù)最小二乘法,由表2的數(shù)據(jù)計算![]() 關于
關于![]() 的回歸方程
的回歸方程![]() ;
;
(Ⅲ)該測試團隊認為:駕駛員酒后駕車的平均“停車距離”![]() 大于(Ⅰ)中無酒狀態(tài)下的停車距離平均數(shù)的3倍,則認定駕駛員是“醉駕”.請根據(jù)(Ⅱ)中的回歸方程,預測當每毫升血液酒精含量大于多少毫克時為“醉駕”?
大于(Ⅰ)中無酒狀態(tài)下的停車距離平均數(shù)的3倍,則認定駕駛員是“醉駕”.請根據(jù)(Ⅱ)中的回歸方程,預測當每毫升血液酒精含量大于多少毫克時為“醉駕”?
(附:對于一組數(shù)據(jù)![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,準線
,準線![]() 的方程為
的方程為![]() .若三角形
.若三角形![]() 的三個頂點都在拋物線
的三個頂點都在拋物線![]() 上,且
上,且![]() ,則稱該三角形為“向心三角形”.
,則稱該三角形為“向心三角形”.
(1)是否存在“向心三角形”,其中兩個頂點的坐標分別為![]() 和
和![]() ?說明理由;
?說明理由;
(2)設“向心三角形”![]() 的一邊
的一邊![]() 所在直線的斜率為
所在直線的斜率為![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)已知三角形![]() 是“向心三角形”,證明:點
是“向心三角形”,證明:點![]() 的橫坐標小于
的橫坐標小于![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】
在平面直角坐標系xOy中,曲線C的參數(shù)方程為![]() (a為參數(shù)),在以原點為極點,x軸正半軸為極軸的極坐標系中,直線l的極坐標方程為
(a為參數(shù)),在以原點為極點,x軸正半軸為極軸的極坐標系中,直線l的極坐標方程為![]() .
.
(1)求C的普通方程和l的傾斜角;
(2)設點![]() ,l和C交于A,B兩點,求
,l和C交于A,B兩點,求![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com