
已知圓C的半徑為1,圓心C在直線l1: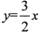 上,且其橫坐標為整數,又圓C截直線
上,且其橫坐標為整數,又圓C截直線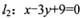 所得的弦長為
所得的弦長為 •
•
(I )求圓C的標準方程;
(II)設動點P在直線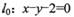 上,過點P作圓的兩條切線PA, PB,切點分別為A ,B求四邊形PACB面積的最小值.
上,過點P作圓的兩條切線PA, PB,切點分別為A ,B求四邊形PACB面積的最小值.
 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| OC |
| OA |
| OB |
| 1 | ||
cos
|
| 1 | ||
cos
|
查看答案和解析>>
科目:高中數學 來源:2010年遼寧省東北育才學校高一下學期期中考試數學試題 題型:解答題
(本題滿分12分)如圖,已知圓O的半徑為1,點C在直徑AB的延長線上,BC=1,點P是圓O上半圓上的一個動點,以PC為邊作正三角形PCD,且點D
與圓心分別在PC兩側.
(1)若 ,試將四邊形OPDC的面積y表示成
,試將四邊形OPDC的面積y表示成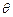 的函數;
的函數;
(2)求四邊形OPDC面積的最大值.
查看答案和解析>>
科目:高中數學 來源:2010年高考試題(全國卷1)解析版(理) 題型:選擇題
已知圓O的半徑為1,PA、PB為該圓的兩條切線,A、B為倆切點,那么 的最小值為
的最小值為
(A)
 (B)
(B) (C)
(C)  (D)
(D)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com