
 的前n項和為Tn,是否存在正整數p,q,使不等式
的前n項和為Tn,是否存在正整數p,q,使不等式 對一切n∈N*都成立?若存在,求出p,q的值;若不存在,說明理由.
對一切n∈N*都成立?若存在,求出p,q的值;若不存在,說明理由.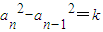 (k為與n無關的常數),從而可得an=b必為一常數數列;若數列{an}是等比數列,利用{an}也是等方差數列,應有
(k為與n無關的常數),從而可得an=b必為一常數數列;若數列{an}是等比數列,利用{an}也是等方差數列,應有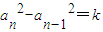 (k為與n無關的常數),可得q=±1,再驗證即可;
(k為與n無關的常數),可得q=±1,再驗證即可;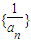 的前n項和,再假設存在正整數p,q,使不等式
的前n項和,再假設存在正整數p,q,使不等式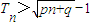 對一切n∈N*都成立,猜想p=q=1,再進行證明.
對一切n∈N*都成立,猜想p=q=1,再進行證明.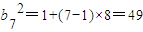 ,∴b7=±7------------------------------(3分)
,∴b7=±7------------------------------(3分)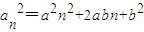 ,
,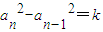 (k為與n無關的常數),得a2=0,即a=0,這時an=b必為一常數數列,因此不存在一個非常數數列的等差數列,同時也是等方差數列.-----(5分)
(k為與n無關的常數),得a2=0,即a=0,這時an=b必為一常數數列,因此不存在一個非常數數列的等差數列,同時也是等方差數列.-----(5分)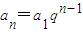 (q為公比且q≠0),則
(q為公比且q≠0),則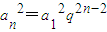 ,
,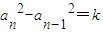 (k為與n無關的常數),即
(k為與n無關的常數),即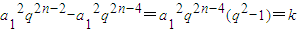 ,所以必有q2=1,q=±1,----------(7分)
,所以必有q2=1,q=±1,----------(7分)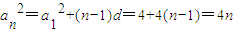 ,
,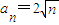 ,------(10分)
,------(10分)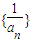 的前n項和為:
的前n項和為: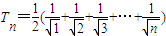 ---(11分)
---(11分)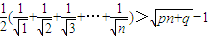 對一切n∈N*都成立.
對一切n∈N*都成立.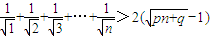
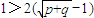 ,∴
,∴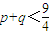 ,又p,q為正整數,∴p=q=1.--(13分)
,又p,q為正整數,∴p=q=1.--(13分)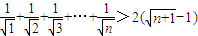 對一切n∈N*都成立.
對一切n∈N*都成立.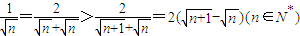
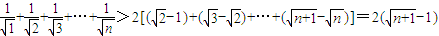 .(16分)
.(16分)

 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| an |
| pn+q |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年北京市朝陽區高三(上)期中數學試卷(文科)(解析版) 題型:解答題
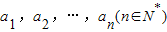 ,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1-c|,|a2-c|,…,|an-c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”
,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1-c|,|a2-c|,…,|an-c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com