已知函數f(x)=x+alnx,其中a為常數,且a≤-1.
(Ⅰ)當a=-1時,求f(x)在[e,e2](e=2.718 28…)上的值域;
(Ⅱ)若f(x)≤e-1對任意x∈[e,e2]恒成立,求實數a的取值范圍.
【答案】
分析:(Ⅰ)求函數f(x)=x-lnx的導數,利用導數判斷在[e,e
2]上的單調性,便可求值域;
(Ⅱ)依題意就是求f(x)在[e,e
2]上的最大值,用a表示出函數最大值,再將恒成立轉化為函數最值問題,結合導數法解決即可.
解答:解:(Ⅰ)當a=-1時,f(x)=x-lnx,
得

,(2分)
令f'(x)>0,即
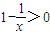
,解得x>1,所以函數f(x)在(1,+∞)上為增函數,
據此,函數f(x)在[e,e
2]上為增函數,(4分)
而f(e)=e-1,f(e
2)=e
2-2,所以函數f(x)在[e,e
2]上的值域為[e-1,e
2-2](6分)
(Ⅱ)由
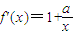
,令f'(x)=0,得
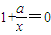
,即x=-a,
當x∈(0,-a)時,f'(x)<0,函數f(x)在(0,-a)上單調遞減;
當x∈(-a,+∞)時,f'(x)>0,函數f(x)在(-a,+∞)上單調遞增;(7分)
若1≤-a≤e,即-e≤a≤-1,易得函數f(x)在[e,e
2]上為增函數,
此時,f(x)
max=f(e
2),要使f(x)≤e-1對x∈[e,e
2]恒成立,只需f(e
2)≤e-1即可,
所以有e
2+2a≤e-1,即
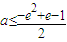
而
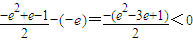
,即
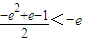
,所以此時無解.(8分)
若e<-a<e
2,即-e>a>-e
2,易知函數f(x)在[e,-a]上為減函數,在[-a,e
2]上為增函數,
要使f(x)≤e-1對x∈[e,e
2]恒成立,只需

,即
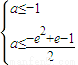
,
由
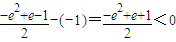
和
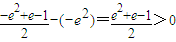
得

.(10分)
若-a≥e
2,即a≤-e
2,易得函數f(x)在[e,e
2]上為減函數,
此時,f(x)
max=f(e),要使f(x)≤e-1對x∈[e,e
2]恒成立,只需f(e)≤e-1即可,
所以有e+a≤e-1,即a≤-1,又因為a≤-e
2,所以a≤-e
2.(12分)
綜合上述,實數a的取值范圍是
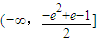
.(13分)
點評:本題考查函數的導數研究函數的單調性,以及函數的導數在求函數最值的應用,解題的關鍵是將恒成立問題轉化為函數最值問題解決,屬于中檔題.

 ,(2分)
,(2分)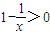 ,解得x>1,所以函數f(x)在(1,+∞)上為增函數,
,解得x>1,所以函數f(x)在(1,+∞)上為增函數,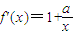 ,令f'(x)=0,得
,令f'(x)=0,得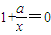 ,即x=-a,
,即x=-a,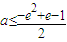
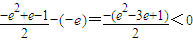 ,即
,即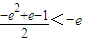 ,所以此時無解.(8分)
,所以此時無解.(8分) ,即
,即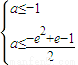 ,
,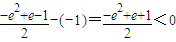 和
和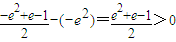
 .(10分)
.(10分)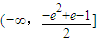 .(13分)
.(13分)

 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<