
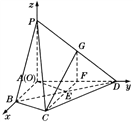
【題目】如圖,四棱錐P-ABCD中, PA⊥平面ABCD,E為BD的中點,G為PD的中點,△DAB≌△DCB,EA=EB=AB=1, ![]() ,連接CE并延長交AD于F.
,連接CE并延長交AD于F.
(Ⅰ)求證:AD⊥CG;
(Ⅱ)求平面BCP與平面DCP的夾角的余弦值.

【答案】(Ⅰ)證明見解析;(Ⅱ) ![]() .
.
【解析】試題分析:(1)根據平幾知識得三角形全等得EF⊥AD,再根據條件PA⊥平面ABCD,得GF⊥AD,根據線面垂直判定定理得AD⊥平面CFG,即得結論,(2)先根據條件建立空間直角坐標系,設立各點坐標,利用方程組解各面法向量,根據向量數量積求向量夾角,最后根據二面角與向量夾角之間關系求結果.
試題解析:(Ⅰ)在△ABD中,因為點E是BD的中點,
∴EA=EB=ED=AB=1,
故![]()
因為△DAB≌△DCB,∴△EAB≌△ECB,
從而有![]()
∴![]() ,故EF⊥AD,AF=FD.
,故EF⊥AD,AF=FD.
又PG=GD,∴FG//PA.又PA⊥平面ABCD,
∴GF⊥AD,故AD⊥平面CFG
又![]() 平面CFG,∴AD⊥CF
平面CFG,∴AD⊥CF
(Ⅱ)以點A為坐標原點建立如圖所示的坐標系,則
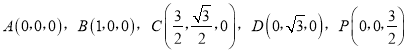
故![]() ,
, ![]() ,
,
![]() .
.
設平面BCP的法向量![]() ,
,
則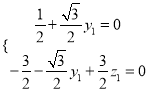 ,解得
,解得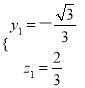 ,
,
即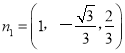
設平面DCP的法向量![]() ,
,
則 解得
解得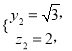
即![]() .從而平面BCP與平面DCP的夾角的余弦值為
.從而平面BCP與平面DCP的夾角的余弦值為
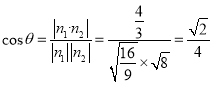


 名題金卷系列答案
名題金卷系列答案 優加精卷系列答案
優加精卷系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直角坐標系中動點![]() ,參數
,參數![]() ,在以原點為極點、
,在以原點為極點、![]() 軸正半軸為極軸所建立的極坐標系中,動點
軸正半軸為極軸所建立的極坐標系中,動點![]() 在曲線
在曲線![]() :
: ![]() 上.
上.
(1)求點![]() 的軌跡
的軌跡![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若動點![]() 的軌跡
的軌跡![]() 和曲線
和曲線![]() 有兩個公共點,求實數
有兩個公共點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形的面積可無限接近圓的面積,并創立了“割圓術”,利用“割圓術”,劉徽得到了圓周率精確到小數點后兩位的近似值3.14,這就是著名的“徽率”,利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出的值為( )
(參考數據: ![]() )
)
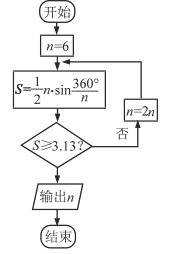
A. 12 B. 24 C. 48 D. 96
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了準確把握市場,做好產品計劃,特對某產品做了市場調查:先銷售該產品50天,統計發現每天的銷售量![]() 分布在
分布在![]() 內,且銷售量
內,且銷售量![]() 的分布頻率滿足:
的分布頻率滿足: 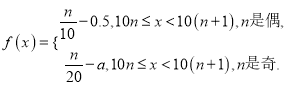
(1)求![]() 的值并估計銷售量的平均數;
的值并估計銷售量的平均數;
(2)若銷售量大于等于80,則稱該日暢銷,其余為滯銷.在暢銷日中用分層抽樣的方法隨機抽取6天,再從這6天中隨機抽取3天進行統計,求這3天不都來自同一組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() ,直線
,直線![]() .
.
(1)以原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系,求圓
軸正半軸為極軸建立極坐標系,求圓![]() 和直線
和直線![]() 的交點的極坐標;
的交點的極坐標;
(2)若點![]() 為圓
為圓![]() 和直線
和直線![]() 交點的中點,且直線
交點的中點,且直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),求
為參數),求![]() ,
, ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以平面直角坐標系的原點為極點,
為參數),以平面直角坐標系的原點為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 的普通方程,并說明其表示什么軌跡;
的普通方程,并說明其表示什么軌跡;
(2)若直線![]() 的極坐標方程為
的極坐標方程為![]() ,試判斷直線
,試判斷直線![]() 與曲線
與曲線![]() 的位置關系,若相交,請求出其弦長.
的位置關系,若相交,請求出其弦長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com