
。】若函數![]() 在區間
在區間![]() 上的圖象為連續不斷的一條曲線,
上的圖象為連續不斷的一條曲線,
則下列說法正確的是( )
A.若![]() ,不存在實數
,不存在實數![]() 使得
使得![]() ;
;
B.若![]() ,存在且只存在一個實數
,存在且只存在一個實數![]() 使得
使得![]() ;
;
C.若![]() ,有可能存在實數
,有可能存在實數![]() 使得
使得![]() ;
;
D.若![]() ,有可能不存在實數
,有可能不存在實數![]() 使得
使得![]() ;
;
科目:高中數學 來源:2012年全國普通高等學校招生統一考試文科數學(湖南卷解析版) 題型:解答題
已知函數f(x)=ex-ax,其中a>0.
(1)若對一切x∈R,f(x)  1恒成立,求a的取值集合;
1恒成立,求a的取值集合;
(2)在函數f(x)的圖像上去定點A(x1, f(x1)),B(x2, f(x2))(x1<x2),記直線AB的斜率為k,證明:存在x0∈(x1,x2),使 恒成立.
恒成立.
【解析】解: 令
令 .
.
當 時
時 單調遞減;當
單調遞減;當 時
時 單調遞增,故當
單調遞增,故當 時,
時, 取最小值
取最小值
于是對一切 恒成立,當且僅當
恒成立,當且僅當 . ①
. ①
令 則
則
當 時,
時, 單調遞增;當
單調遞增;當 時,
時, 單調遞減.
單調遞減.
故當 時,
時, 取最大值
取最大值 .因此,當且僅當
.因此,當且僅當 時,①式成立.
時,①式成立.
綜上所述, 的取值集合為
的取值集合為 .
.
(Ⅱ)由題意知, 令
令 則
則


令 ,則
,則 .當
.當 時,
時, 單調遞減;當
單調遞減;當 時,
時, 單調遞增.故當
單調遞增.故當 ,
, 即
即
從而 ,
, 又
又

所以
 因為函數
因為函數 在區間
在區間 上的圖像是連續不斷的一條曲線,所以存在
上的圖像是連續不斷的一條曲線,所以存在 使
使 即
即 成立.
成立.
【點評】本題考查利用導函數研究函數單調性、最值、不等式恒成立問題等,考查運算能力,考查分類討論思想、函數與方程思想等數學方法.第一問利用導函數法求出 取最小值
取最小值 對一切x∈R,f(x)
對一切x∈R,f(x)  1恒成立轉化為
1恒成立轉化為 從而得出求a的取值集合;第二問在假設存在的情況下進行推理,然后把問題歸結為一個方程是否存在解的問題,通過構造函數,研究這個函數的性質進行分析判斷.
從而得出求a的取值集合;第二問在假設存在的情況下進行推理,然后把問題歸結為一個方程是否存在解的問題,通過構造函數,研究這個函數的性質進行分析判斷.
查看答案和解析>>
科目:高中數學 來源:2012屆云南省高三上期中文科數學試卷(解析版) 題型:填空題
(本題滿分12分)已知函數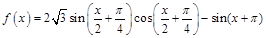 。
。
(1)求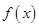 的最小正周期;
的最小正周期;
(2)若將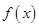 的圖象向右平移
的圖象向右平移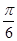 個單位,得到函數
個單位,得到函數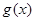 的圖象,求函數
的圖象,求函數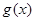 在區間
在區間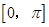 上的最大值和最小值。
上的最大值和最小值。
【解析】第一問中主要利用三角函數的兩角和差公式化簡為單一三角函數解析式
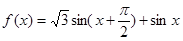 =
=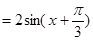
然后利用周期公式得到第一問。
第二問中,由于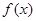 的圖象向右平移
的圖象向右平移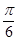 個單位,得到函數
個單位,得到函數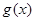 的圖象,
的圖象,
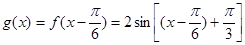
然后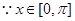 時,
時,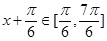 結合三角函數值域求解得到范圍。
結合三角函數值域求解得到范圍。
查看答案和解析>>
科目:高中數學 來源:2013屆浙江杭州七校高二下期期中理科數學試卷(解析版) 題型:解答題
已知函數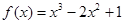 .
.
(1)求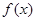 在區間
在區間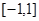 上的最大值;
上的最大值;
(2)若函數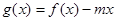 在區間
在區間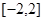 上存在遞減區間,求實數m的取值范圍.
上存在遞減區間,求實數m的取值范圍.
【解析】本試題主要考查了導數在研究函數中的運用,求解函數的最值。第一問中,利用導數求解函數的最值,首先求解導數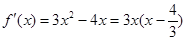 ,然后利用極值和端點值比較大小,得到結論。第二問中,我們利用函數在
,然后利用極值和端點值比較大小,得到結論。第二問中,我們利用函數在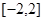 上存在遞減區間,即
上存在遞減區間,即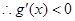 在
在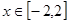 上有解,即
上有解,即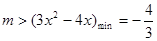 ,即可,可得到。
,即可,可得到。
解:(1)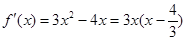 ,
,
令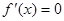 ,解得
,解得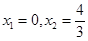 ……………3分
……………3分
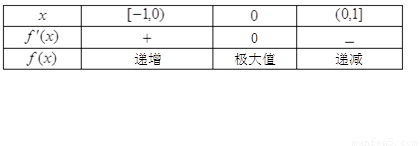
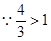 ,
,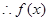 在
在 上為增函數,在
上為增函數,在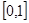 上為減函數,
上為減函數,
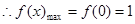 .
…………6分
.
…………6分
(2)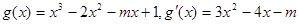
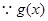 在
在 上存在遞減區間,
上存在遞減區間,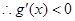 在
在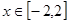 上有解,……9分
上有解,……9分
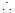
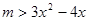 在
在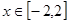 上有解,
上有解,
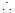
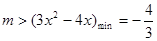 ,
,
所以,實數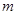 的取值范圍為
的取值范圍為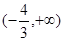
查看答案和解析>>
科目:高中數學 來源:2013屆浙江寧波四校高二下學期期中聯考理科數學試卷(解析版) 題型:解答題
已知函數
(1) 若函數 在
在 上單調,求
上單調,求 的值;
的值;
(2)若函數 在區間
在區間 上的最大值是
上的最大值是 ,求
,求 的取值范圍.
的取值范圍.
【解析】第一問,

 ,
,  、
、
第二問中,
由(1)知: 當 時,
時,  上單調遞增
上單調遞增

 滿足條件當
滿足條件當 時,
時, 
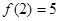


解: (1) 
 ……3分
……3分
 ,
,  …………….7分
…………….7分
(2) 
由(1)知: 當 時,
時,  上單調遞增
上單調遞增

 滿足條件…………..10分
滿足條件…………..10分
當 時,
時,  且
且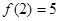

 …………13分
…………13分
綜上所述: 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com