
【題目】若函數![]() 對定義域內的每一個值
對定義域內的每一個值![]() ,在其定義域內都存在唯一的
,在其定義域內都存在唯一的![]() ,使
,使![]() 成立,則該函數為“依附函數”.
成立,則該函數為“依附函數”.
(1)判斷函數![]() 是否為“依附函數”,并說明理由;
是否為“依附函數”,并說明理由;
(2)若函數![]() 在定義域
在定義域![]() 上“依附函數”,求
上“依附函數”,求![]() 的取值范圍;
的取值范圍;
(3)已知函數![]() 在定義域
在定義域![]() 上為“依附函數”.若存在實數
上為“依附函數”.若存在實數![]() ,使得對任意的
,使得對任意的![]() ,不等式
,不等式![]() 都成立,求實數
都成立,求實數![]() 的最大值.
的最大值.
【答案】(1)不是,理由見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)舉出反例:取![]() ,但是不存在
,但是不存在![]() ,即可判定;
,即可判定;
(2)根據依附函數的關系,結合![]() 在
在![]() 遞增,故
遞增,故![]() ,即
,即![]() ,
,![]() ,
,![]() 即可求得取值范圍;
即可求得取值范圍;
(3)根據依附函數的關系結合單調性分析可得![]() ,將問題轉化為存在
,將問題轉化為存在![]() ,使得對任意的
,使得對任意的![]() ,有不等式
,有不等式![]() 都成立,即關于t的不等式
都成立,即關于t的不等式![]() 恒成立,即可求解.
恒成立,即可求解.
(1)對于函數![]() 的定義域
的定義域![]() 內存在
內存在![]() ,則
,則![]() ,無解.
,無解.
故![]() 不是“依附函數”;
不是“依附函數”;
(2)因為![]() 在
在![]() 遞增,故
遞增,故![]() ,
,
即![]() ,
,![]() ,
,
由![]() ,故
,故![]() ,得
,得![]() ,
,
從而![]() 在
在![]() 上單調遞增,故
上單調遞增,故![]() ,
,
(3)①若![]() ,故
,故![]() 在
在![]() 上最小值為0,此時不存在
上最小值為0,此時不存在![]() ,舍去;
,舍去;
②若![]() 故
故![]() 在
在![]() 上單調遞減,從而
上單調遞減,從而![]() ,
,
解得![]() (舍)或
(舍)或![]() .從而,存在
.從而,存在![]() ,使得對任意的
,使得對任意的![]() ,
,
有不等式![]() 都成立,
都成立,
即![]() 恒成立,
恒成立,
由![]() ,得
,得![]() ,
,
由![]() ,可得
,可得![]() ,
,
又![]() 在
在![]() 單調遞減,
單調遞減,
故當![]() 時,
時,![]() ,
,
從而![]() ,解得
,解得![]() ,
,
綜上,故實數![]() 的最大值為
的最大值為![]() .
.


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
【題目】用![]() 代表紅球,
代表紅球,![]() 代表藍球,
代表藍球,![]() 代表黑球,由加法原理及乘法原理,從1個紅球和1個藍球中取出若干個球的所有取法可由
代表黑球,由加法原理及乘法原理,從1個紅球和1個藍球中取出若干個球的所有取法可由![]() 的展開式
的展開式![]() 表示出來,如:“1”表示一個球都不取、“
表示出來,如:“1”表示一個球都不取、“![]() ”表示取出一個紅球,而“
”表示取出一個紅球,而“![]() ”用表示把紅球和藍球都取出來.以此類推,下列各式中,其展開式可用來表示從5個有區別的紅球、5個無區別的藍球、5個無區別的黑球中取出若干個球,且所有的藍球都取出或都不取出的所有取法的是( )
”用表示把紅球和藍球都取出來.以此類推,下列各式中,其展開式可用來表示從5個有區別的紅球、5個無區別的藍球、5個無區別的黑球中取出若干個球,且所有的藍球都取出或都不取出的所有取法的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,以原點為極點,以![]() 軸的非負半軸為極軸且取相同的單位長度建立極坐標系,曲線
軸的非負半軸為極軸且取相同的單位長度建立極坐標系,曲線![]() 的極坐標方程為:
的極坐標方程為:![]() .
.
(1)若曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),求曲線
為參數),求曲線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的普通方程;
的普通方程;
(2)若曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),
為參數),![]() ,且曲線
,且曲線![]() 與曲線
與曲線![]() 的交點分別為
的交點分別為![]() 、
、![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據中國日報網報道:2017年11月13日,TOP500發布的最新一期全球超級計算機500強榜單顯示,中國超算在前五名中占據兩席,其中超算全球第一“神威太湖之光”完全使用了國產品牌處理器。為了了解國產品牌處理器打開文件的速度,某調查公司對兩種國產品牌處理器進行了12次測試,結果如下(數值越小,速度越快,單位是MIPS)
測試1 | 測試2 | 測試3 | 測試4 | 測試5 | 測試6 | 測試7 | 測試8 | 測試9 | 測試10 | 測試11 | 測試12 | |
品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
設![]() 分別表示第次測試中品牌A和品牌B的測試結果,記
分別表示第次測試中品牌A和品牌B的測試結果,記![]()
![]()
(Ⅰ)求數據![]() 的眾數;
的眾數;
(Ⅱ)從滿足![]() 的測試中隨機抽取兩次,求品牌A的測試結果恰好有一次大于品牌B的測試結果的概率;
的測試中隨機抽取兩次,求品牌A的測試結果恰好有一次大于品牌B的測試結果的概率;
(Ⅲ)經過了解,前6次測試是打開含有文字和表格的文件,后6次測試是打開含有文字和圖片的文件.請你依據表中數據,運用所學的統計知識,對這兩種國產品牌處理器打開文件的速度進行評價.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】p:關于x的方程![]() 無解,q:
無解,q:![]() (
(![]() )
)
(1)若![]() 時,“
時,“![]() ”為真命題,“
”為真命題,“![]() ”為假命題,求實數a的取值范圍.
”為假命題,求實數a的取值范圍.
(2)當命題“若p,則q”為真命題,“若q,則p”為假命題時,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,拋物線關于![]() 軸對稱,它的頂點在坐標原點,點
軸對稱,它的頂點在坐標原點,點![]() 、
、![]() 、
、![]() 均在拋物線上.
均在拋物線上.
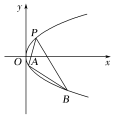
(1)寫出該拋物線的方程及其準線方程;
(2)當![]() 與
與![]() 的斜率存在且傾斜角互補時,求
的斜率存在且傾斜角互補時,求![]() 的值及直線
的值及直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在高一某班的元旦文藝晚會中,有這么一個游戲:一盒子內裝有6張大小和形狀完全相同的卡片,每張卡片上寫有一個成語,它們分別為意氣風發、風平浪靜、心猿意馬、信馬由韁、氣壯山河、信口開河,從盒內隨機抽取2張卡片,若這2張卡片上的2個成語有相同的字就中獎,則該游戲的中獎率為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數![]() 是奇函數.
是奇函數.
(1)求實數a的值;
(2)判斷該函數在定義域R上的單調性(不要求寫證明過程).
(3)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數k的取值范圍;
恒成立,求實數k的取值范圍;
(4)設關于x的函數![]() 有零點,求實數b的取值范圍.
有零點,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 滿足以下4個條件.
滿足以下4個條件.
①函數![]() 的定義域是
的定義域是![]() ,且其圖象是一條連續不斷的曲線;
,且其圖象是一條連續不斷的曲線;
②函數![]() 在
在![]() 不是單調函數;
不是單調函數;
③函數![]() 是偶函數;
是偶函數;
④函數![]() 恰有2個零點.
恰有2個零點.
(1)寫出函數![]() 的一個解析式;
的一個解析式;
(2)畫出所寫函數![]() 的解析式的簡圖;
的解析式的簡圖;
(3)證明![]() 滿足結論③及④.
滿足結論③及④.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com