
【題目】已知![]() ,命題
,命題![]() :對(duì)
:對(duì)![]() ,不等式
,不等式![]() 恒成立;命題
恒成立;命題![]() ,使得
,使得![]() 成立.
成立.
(1)若![]() 為真命題,求
為真命題,求![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() 時(shí),若
時(shí),若![]() 假,
假, ![]() 為真,求
為真,求![]() 的取值范圍.
的取值范圍.
【答案】(1) 1≤m≤2.(2) (﹣∞,1)∪(1,2].
【解析】試題分析:本題主要考查簡(jiǎn)易邏輯,恒成立問(wèn)題,不等式的解法.(1)由題意得出![]() ,然后解不等式即可.(2)由題意得出
,然后解不等式即可.(2)由題意得出![]() ,再根據(jù)p且q為假,p或q為真,得出p與q必然一真一假,即可解答.
,再根據(jù)p且q為假,p或q為真,得出p與q必然一真一假,即可解答.
試題解析:
(1)設(shè)![]() ,則
,則![]() 在[0,1]上單調(diào)遞增,
在[0,1]上單調(diào)遞增,
∴![]() .
.
∵對(duì)任意x∈[0,1],不等式2x﹣2≥m2﹣3m恒成立,
∴![]() ,即
,即![]() ,
,
解得1≤m≤2.
∴![]() 的取值范圍為
的取值范圍為![]() .
.
(2)a=1時(shí), ![]() 區(qū)間[﹣1,1]上單調(diào)遞增,
區(qū)間[﹣1,1]上單調(diào)遞增,
∴![]() .
.
∵存在x∈[﹣1,1],使得m≤ax成立,
∴m≤1.
∵![]() 假,
假, ![]() 為真,
為真,
∴p與q一真一假,
①當(dāng)p真q假時(shí),
可得![]() ,解得1<m≤2;
,解得1<m≤2;
②當(dāng)p假q真時(shí),
可得![]() ,解得
,解得![]() .
.
綜上可得1<m≤2或m<1.
∴實(shí)數(shù)m的取值范圍是(﹣∞,1)∪(1,2].


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)若函數(shù)![]() 在定義域上是增函數(shù),求實(shí)數(shù)
在定義域上是增函數(shù),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)若![]() ,令
,令![]() ,試討論函數(shù)
,試討論函數(shù)![]() 的零點(diǎn)個(gè)數(shù),并說(shuō)明理由.
的零點(diǎn)個(gè)數(shù),并說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】根據(jù)國(guó)家環(huán)保部新修訂的《環(huán)境空氣質(zhì)量標(biāo)準(zhǔn)》規(guī)定:居民區(qū)![]() 的年平均濃度不得超過(guò)3S微克/立方米,
的年平均濃度不得超過(guò)3S微克/立方米, ![]() 的24小時(shí)平均濃度不得超過(guò)75微克/立方米.某市環(huán)保局隨機(jī)抽取了一居民區(qū)2016年20天
的24小時(shí)平均濃度不得超過(guò)75微克/立方米.某市環(huán)保局隨機(jī)抽取了一居民區(qū)2016年20天![]() 的24小時(shí)平均濃度(單位:微克/立方米)的監(jiān)測(cè)數(shù)據(jù),數(shù)據(jù)統(tǒng)計(jì)如圖表:
的24小時(shí)平均濃度(單位:微克/立方米)的監(jiān)測(cè)數(shù)據(jù),數(shù)據(jù)統(tǒng)計(jì)如圖表:
組別 |
| 頻數(shù)(天) | 頻率 |
第一組 |
| 3 | 0.15 |
第二組 |
| 12 | 0.6 |
第三組 |
| 3 | 0.15 |
第四組 |
| 2 | 0.1 |
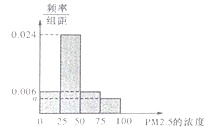
(Ⅰ)將這20天的測(cè)量結(jié)果按表中分組方法繪制成的樣本頻率分布直方圖如圖.
(ⅰ)求圖中![]() 的值;
的值;
(ⅱ)在頻率分布直方圖中估算樣本平均數(shù),并根據(jù)樣本估計(jì)總體的思想,從![]() 的年平均度考慮,判斷該居民區(qū)的環(huán)境質(zhì)量是否需要改善?并說(shuō)明理由.
的年平均度考慮,判斷該居民區(qū)的環(huán)境質(zhì)量是否需要改善?并說(shuō)明理由.
(Ⅱ)將頻率視為概率,對(duì)于2016年的某3天,記這3天中該居民區(qū)![]() 的24小時(shí)平均濃度符合環(huán)境空氣質(zhì)量標(biāo)準(zhǔn)的天數(shù)為
的24小時(shí)平均濃度符合環(huán)境空氣質(zhì)量標(biāo)準(zhǔn)的天數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】△ABC的內(nèi)角A,B,C的對(duì)邊分別為a,b,c,已知![]() .
.
(1)求C;
(2)若c=![]() ,△ABC的面積為
,△ABC的面積為![]() ,求△ABC的周長(zhǎng).
,求△ABC的周長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]()
(1)求函數(shù)![]() 的單調(diào)增區(qū)間;
的單調(diào)增區(qū)間;
(2)當(dāng)![]() 時(shí),記
時(shí),記![]() ,是否存在整數(shù)
,是否存在整數(shù)![]() ,使得關(guān)于
,使得關(guān)于![]() 的不等式
的不等式![]() 有解?若存在,請(qǐng)求出
有解?若存在,請(qǐng)求出![]() 的最小值;若不存在,請(qǐng)說(shuō)明理由.
的最小值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】直線(xiàn)![]() 與雙曲線(xiàn)
與雙曲線(xiàn)![]() 的漸近線(xiàn)交于
的漸近線(xiàn)交于![]() 兩點(diǎn),設(shè)
兩點(diǎn),設(shè)![]() 為雙曲線(xiàn)上任一點(diǎn),若
為雙曲線(xiàn)上任一點(diǎn),若![]() 為坐標(biāo)原點(diǎn)),則下列不等式恒成立的是( )
為坐標(biāo)原點(diǎn)),則下列不等式恒成立的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了響應(yīng)我市“創(chuàng)建宜居港城,建設(shè)美麗莆田”,某環(huán)保部門(mén)開(kāi)展以“關(guān)愛(ài)木蘭溪,保護(hù)母親河”為主題的環(huán)保宣傳活動(dòng),將木蘭溪流經(jīng)市區(qū)河段分成![]() 段,并組織青年干部職工對(duì)每一段的南、北兩岸進(jìn)行環(huán)保綜合測(cè)評(píng),得到分值數(shù)據(jù)如下表:
段,并組織青年干部職工對(duì)每一段的南、北兩岸進(jìn)行環(huán)保綜合測(cè)評(píng),得到分值數(shù)據(jù)如下表:
南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
(Ⅰ)記評(píng)分在![]() 以上(包括
以上(包括![]() )為優(yōu)良,從中任取一段,求在同一段中兩岸環(huán)保評(píng)分均為優(yōu)良的概率;
)為優(yōu)良,從中任取一段,求在同一段中兩岸環(huán)保評(píng)分均為優(yōu)良的概率;
(Ⅱ)根據(jù)表中數(shù)據(jù)完成下面莖葉圖;
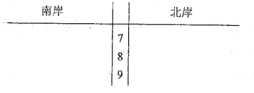
(Ⅲ)分別估計(jì)兩岸分值的中位數(shù),并計(jì)算它們的平均值,試從計(jì)算結(jié)果分析兩岸環(huán)保情況,哪邊保護(hù)更好.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓G: ![]() 的離心率為
的離心率為![]() ,過(guò)橢圓G右焦點(diǎn)F的直線(xiàn)m:x=1與橢圓G交于點(diǎn)M(點(diǎn)M在第一象限).
,過(guò)橢圓G右焦點(diǎn)F的直線(xiàn)m:x=1與橢圓G交于點(diǎn)M(點(diǎn)M在第一象限).
(Ⅰ)求橢圓G的方程;
(Ⅱ)已知A為橢圓G的左頂點(diǎn),平行于AM的直線(xiàn)l與橢圓G相交于B,C兩點(diǎn),請(qǐng)判斷直線(xiàn)MB,MC是否關(guān)于直線(xiàn)m對(duì)稱(chēng),并說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知雙曲線(xiàn)E: ![]() (a>0,b>0)的漸近線(xiàn)方程為3x±4y=0,且過(guò)焦點(diǎn)垂直x軸的直線(xiàn)與雙曲線(xiàn)E相交弦長(zhǎng)為
(a>0,b>0)的漸近線(xiàn)方程為3x±4y=0,且過(guò)焦點(diǎn)垂直x軸的直線(xiàn)與雙曲線(xiàn)E相交弦長(zhǎng)為![]() ,過(guò)雙曲線(xiàn)E中心的直線(xiàn)與雙曲線(xiàn)E交于A,B兩點(diǎn),在雙曲線(xiàn)E上取一點(diǎn)C(與A,B不重合),直線(xiàn)AC,BC 的斜率分別為k1,k2,則k1k2等于( )
,過(guò)雙曲線(xiàn)E中心的直線(xiàn)與雙曲線(xiàn)E交于A,B兩點(diǎn),在雙曲線(xiàn)E上取一點(diǎn)C(與A,B不重合),直線(xiàn)AC,BC 的斜率分別為k1,k2,則k1k2等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com