Question

【題目】為了解少年兒童的肥胖是否與常喝碳酸飲料有關，現對40名小學六年級學生進行了問卷調查，并得到如下列聯表.平均每天喝以上為“常喝”，體重超過為“肥胖”.已知在全部40人中隨機抽取1人，抽到肥胖學生的概率為.

	常喝	不常喝	合計
肥胖		3
不肥胖	5
合計			40

（1）請將上面的列聯表補充完整；

（2）是否有的把握認為肥胖與常喝碳酸飲料有關？請說明你的理由.

參考公式：

①卡方統計量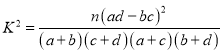，其中為樣本容量；

②獨立性檢驗中的臨界值參考表：

	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

Answer 1

【答案】（1）列聯表見解析；（2）有的把握認為肥胖與常喝碳酸飲料有關.

【解析】

（1）由抽到肥胖學生的概率為可知肥胖的學生有10人,進而補全列聯表即可；

（2）利用公式求得的值,與7.879比較即可判斷

（1）設肥胖學生共名,則,解得,

∴肥胖學生共有10名,

則列聯表如下:

	常喝	不常喝	合計
肥胖	7	3	10
不肥胖	5	25	30
合計	12	28	40

（2）由已知數據可求得,,

因此,有的把握認為肥胖與常喝碳酸飲料有關.