
如圖,四棱錐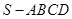 的底面是正方形,
的底面是正方形, ⊥平面
⊥平面 ,
,
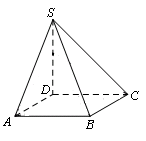
(1)求證: ;
;
(2)求二面角 的大小.
的大小.
(1)證明見解析;(2)  .
.
【解析】
試題分析:(1)要證線線垂直,一般通過證明線面垂直來實現,那么我們就要尋找圖形中已有哪些與待證線垂直的直線,本題中首先由已知有 ,又有
,又有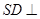 平面
平面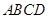 ,則
,則 ,故可證明
,故可證明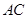 與過
與過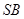 的平面
的平面 垂直,從而得線線垂直;(2)要求二面角的大小,一般須根據定義作出二面角的平面角,在三角形中解出,而平面角就是要與二面角的棱垂直的直線(射線),題中棱是
垂直,從而得線線垂直;(2)要求二面角的大小,一般須根據定義作出二面角的平面角,在三角形中解出,而平面角就是要與二面角的棱垂直的直線(射線),題中棱是 ,在兩個面(半平面)內與
,在兩個面(半平面)內與 垂直的直線是哪個呢?注意到已知
垂直的直線是哪個呢?注意到已知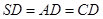 ,因此有
,因此有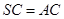 ,從而
,從而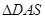 與
與 都是以
都是以 為底邊的等腰三角形,故垂直關系就是取底邊
為底邊的等腰三角形,故垂直關系就是取底邊 中點
中點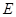 ,根據等腰三角形的性質有
,根據等腰三角形的性質有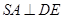 ,
, ,
, 就是我們要找的平面角.
就是我們要找的平面角.
試題解析:(1)連接BD,∵ ⊥平面
⊥平面
 平面
平面
∴AC⊥SD 4分
又四邊形ABCD是正方形,∴AC⊥BD
∴AC ⊥平面SBD
∴AC⊥SB. 6分
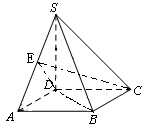
(2)設 的中點為
的中點為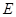 ,連接
,連接 、
、 ,
,
∵SD=AD,CS=CA,
∴DE⊥SA, CE⊥SA.
∴ 是二面角
是二面角 的平面角. 9分
的平面角. 9分
計算得:DE=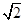 ,CE=
,CE= ,CD=2,則CD⊥DE.
,CD=2,則CD⊥DE.
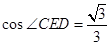 ,
, 
所以所求二面角的大小為 . 12分
. 12分
考點:(1)線線垂直;(2)二面角.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
(09年山東實驗中學診斷三理)(13分)如圖:四棱錐![]() 的底面
的底面![]() 是提醒,腰
是提醒,腰![]() ,
,![]() 平分
平分![]() 且與
且與![]() 垂直,側面
垂直,側面![]() 都垂直于底面,平面
都垂直于底面,平面![]() 與底面
與底面![]() 成60°角
成60°角
![]() (1)求證:
(1)求證:![]() ;
;
![]() (2)求二面角
(2)求二面角![]() 的大小
的大小![]()
![]()
![]()
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省高三第八次月考文科數學試卷 題型:解答題
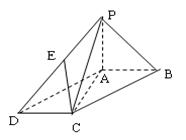
如圖,四棱錐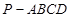 的底面是平行四邊形,
的底面是平行四邊形,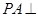 平面
平面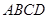 ,
,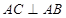 ,
,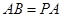 ,
,
點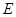 是
是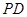 上的點,且
上的點,且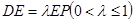 .
.
(Ⅰ)求證: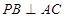 ;
;
(Ⅱ)求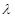 的值,使
的值,使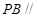 平面
平面 ;
;
(Ⅲ)當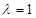 時,求三棱錐
時,求三棱錐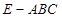 與四棱錐
與四棱錐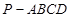 的體積之比.
的體積之比.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省高三上學期摸底理科數學 題型:解答題
((本小題滿分14分)如圖,四棱錐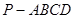 的底面
的底面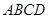 是正方形,側棱
是正方形,側棱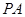
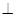 底面
底面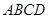 ,
,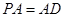 ,
,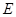 、
、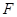 分別是棱
分別是棱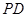 、
、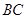 的中點.
的中點.
(1)求證: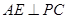 ; (2) 求直線
; (2) 求直線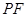 與平面
與平面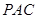 所成的角的正切值
所成的角的正切值
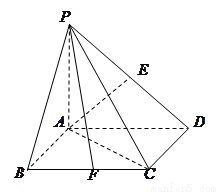
查看答案和解析>>
科目:高中數學 來源:2010-2011年四川省成都市高二3月月考數學試卷 題型:填空題
(本小題滿分12 分)
如圖,四棱錐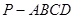 的底面是邊長為
的底面是邊長為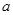 的菱形,
的菱形,
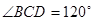 ,
,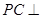 平面
平面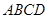 ,
,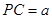 ,
,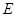 為
為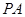 的中點,O為底面對角線的交點;
的中點,O為底面對角線的交點;
(1)求證:平面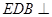 平面
平面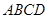 ;
;
(2)求二面角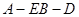 的正切值。
的正切值。
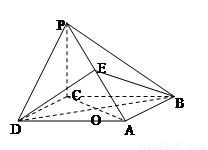
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com