
【題目】已知關于x的不等ax2﹣3x+2>0的解集{x|x<1或x>b}
(Ⅰ)求a,b的值;
(Ⅱ)解關于x的不等式:ax2﹣(ac+b)x+bx<0.
【答案】解:(Ⅰ)∵不等式ax2﹣3x+2>0的解集是{x|x<1或x>b},
∴方程ax2﹣3x+2=0的實數根是1和b,
由根與系數的關系,得;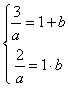
解得a=1,b=2;
(Ⅱ)∵a=1,b=2;
∴不等式ax2﹣(ac+b)x+bx<0化為
x2﹣(c+2)x+2x<0,
即x(x﹣c)<0;
∴當c>0時,解得0<x<c,
當c=0時,不等式無解,
當c<0時,解得c<x<0;
綜上,當c>0時,不等式的解集是(0,c),
當c=0時,不等式的解集是,
當c<0時,不等式的解集是(c,0).
【解析】(Ⅰ)根據不等式ax2﹣3x+2>0的解集,得出方程ax2﹣3x+2=0的實數根,由根與系數的關系,求出a、b的值;(Ⅱ)由a、b的值,化簡不等式ax2﹣(ac+b)x+bx<0,討論c的值,求出不等式的解集即可.
【考點精析】認真審題,首先需要了解解一元二次不等式(求一元二次不等式![]()
![]() 解集的步驟:一化:化二次項前的系數為正數;二判:判斷對應方程的根;三求:求對應方程的根;四畫:畫出對應函數的圖象;五解集:根據圖象寫出不等式的解集;規律:當二次項系數為正時,小于取中間,大于取兩邊).
解集的步驟:一化:化二次項前的系數為正數;二判:判斷對應方程的根;三求:求對應方程的根;四畫:畫出對應函數的圖象;五解集:根據圖象寫出不等式的解集;規律:當二次項系數為正時,小于取中間,大于取兩邊).


科目:高中數學 來源: 題型:
【題目】已知在直角坐標![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的參數方程為:
的參數方程為: 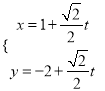 ,曲線
,曲線![]() 的極坐標方程:
的極坐標方程: ![]()
(1)寫出![]() 和
和![]() 的普通方程;
的普通方程;
(2)若![]() 與
與![]() 交于兩點
交于兩點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4;坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).在以坐標原點為極點,
為參數).在以坐標原點為極點, ![]() 軸正半軸為極軸的極坐標中,曲線
軸正半軸為極軸的極坐標中,曲線![]() .
.
(Ⅰ)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程.
的直角坐標方程.
(Ⅱ)求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一元二次不等式﹣x2+x+2>0的解集是( )
A.{x|x<﹣1或x>2}
B.{x|x<﹣2或x>1}
C.{x|﹣1<x<2}
D.{x|﹣2<x<1}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() ,
, ![]() ,則下列說法正確的是( )
,則下列說法正確的是( )
A. 把![]() 上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移
上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
B. 把![]() 上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移
上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
C. 把曲線![]() 向右平移
向右平移![]() 個單位長度,再把得到的曲線上各點橫坐標縮短到原來的
個單位長度,再把得到的曲線上各點橫坐標縮短到原來的![]() ,縱坐標不變,得到曲線
,縱坐標不變,得到曲線![]()
D. 把曲線![]() 向右平移
向右平移![]() 個單位長度,再把得到的曲線上各點橫坐標縮短到原來的
個單位長度,再把得到的曲線上各點橫坐標縮短到原來的![]() ,縱坐標不變,得到曲線
,縱坐標不變,得到曲線![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設向量 ![]() =(cosθ,sinθ),
=(cosθ,sinθ), ![]() =(﹣
=(﹣ ![]() ,
, ![]() );
);
(1)若 ![]() ∥
∥ ![]() ,且θ∈(0,π),求θ;
,且θ∈(0,π),求θ;
(2)若|3 ![]() +
+ ![]() |=|
|=| ![]() ﹣3
﹣3 ![]() |,求|
|,求| ![]() +
+ ![]() |的值.
|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且a1=2,an+1= ![]() Sn(n=1,2,3,…).
Sn(n=1,2,3,…).
(1)證明:數列{ ![]() }是等比數列;
}是等比數列;
(2)設bn= ![]() ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com