
汕頭二中擬建一座長 米,寬
米,寬 米的長方形體育館.按照建筑要求,每隔
米的長方形體育館.按照建筑要求,每隔 米(
米( ,
, 為正常數)需打建一個樁位,每個樁位需花費
為正常數)需打建一個樁位,每個樁位需花費 萬元(樁位視為一點且打在長方形的邊上),樁位之間的
萬元(樁位視為一點且打在長方形的邊上),樁位之間的 米墻面需花
米墻面需花 萬元,在不計地板和天花板的情況下,當
萬元,在不計地板和天花板的情況下,當 為何值時,所需總費用最少?
為何值時,所需總費用最少?
【解析】本試題主要考查了導數在研究函數中的運用。先求需打 個樁位.再求解墻面所需費用為:
個樁位.再求解墻面所需費用為: ,最后表示總費用
,最后表示總費用 ,利用導數判定單調性,求解最值。
,利用導數判定單調性,求解最值。
解:由題意可知,需打 個樁位.
…………………2分
個樁位.
…………………2分
墻面所需費用為: ,……4分
,……4分
∴所需總費用
 (
( )…7分
)…7分
令 ,則
,則
當 時,
時, ;當
;當 時,
時, .
.
∴當 時,
時,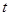 取極小值為
取極小值為 .而在
.而在 內極值點唯一,所以
內極值點唯一,所以 .∴當
.∴當 時,
時, (萬元),即每隔3米打建一個樁位時,所需總費用最小為1170萬元.
(萬元),即每隔3米打建一個樁位時,所需總費用最小為1170萬元.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com