已知集合A={x||x-a|≤1},B={x|x2-5x+4≥0}.
(1)若a=3,求A;
(2)若A∩B=∅,求實數a的取值范圍.
【答案】
分析:(1)只須解當a=3時的絕對值不等式:|x-3|≤1即得集合A;
(2)先化簡集合A:A={x|a-1≤x≤a+1}和集合B,再根據它們的交集的定義得區間端點的不等關系,最后解不等式組即得實數a的取值范圍.
解答:解:(1)當a=3,由|x-3|≤1得-1≤x-3≤1
解得2≤x≤4∴A={x|2≤x≤4}(4分)
(2)由|x-a|≤1得a-1≤x≤a+1∴A={x|a-1≤x≤a+1}.(6分)
由x
2-5x+4≥0解得x≤1或x≥4∴B={x|x≤1或x≥4}.(8分)∵A∩B=∅,
∴
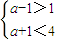
得2<a<3
即a的取值范圍是2<a<3.(12分)
點評:本題主要考查了一元二次不等式的解法、絕對值不等式的解法、集合的包含關系判斷及應用等基礎知識,屬于容易題.

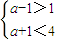 得2<a<3
得2<a<3
