
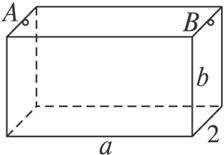
圖1-1-2
分析:依題意可以建立兩個基本的等量關系:①y=![]() (y為質量分數,k為比例系數);②4b+2ab+2a=60.具體求解可有兩條思路:一是將②式變形代入①式消元成一元函數,再求使y取得最小值時的自變量值;二是由①式知y為最小值等價于求ab的最大值,將ab看作一個整體,利用②式去尋求.在求最值的過程中,若遇到變量的和式或積式可考慮運用均值定理.
(y為質量分數,k為比例系數);②4b+2ab+2a=60.具體求解可有兩條思路:一是將②式變形代入①式消元成一元函數,再求使y取得最小值時的自變量值;二是由①式知y為最小值等價于求ab的最大值,將ab看作一個整體,利用②式去尋求.在求最值的過程中,若遇到變量的和式或積式可考慮運用均值定理.
解法一:設y為流出的水中雜質的質量分數,則y=![]() ,其中k>0為比例系數.
,其中k>0為比例系數.
根據題設,有
4b+2ab+2a=60(a>0,b>0),
∴b=![]() (0<a<30).③
(0<a<30).③
于是y=![]() =
= =
=
=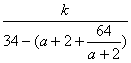
≥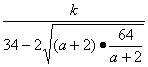 =
=![]() .
.
當a+2=![]() 時取等號,y達到最小值.
時取等號,y達到最小值.
這時a=6或a=-10(舍去).
將a=6代入③式得b=3.
當a為6 m,b為3 m時,經沉淀后流出的水中該雜質的質量分數最小.
解法二:設y為流出的水中雜質的質量分數,則y=![]() ,其中k>0為比例系數.
,其中k>0為比例系數.
依題意,即所求的a、b值使ab最大.
由題設,知4b+2ab+2a=60(a>0,b>0),
即a+2b+ab=30(a>0,b>0).
∵a+2b≥2![]() ,
,
∴2![]()
![]() +ab≤30
+ab≤30![]() ab+2
ab+2![]()
![]() -30≤0
-30≤0![]() (
(![]() +5
+5![]() )(
)(![]() -3
-3![]() )≤0.
)≤0.
當且僅當a=2b時,上式取等號.
當a>0,b>0時,解得0<ab≤18,
即當a=2b時,ab取得最大值為18.
∴2b2=18.解得b=3,則a=6.
故當a為6 m,b為3 m時,經沉淀后流出的水中該雜質的質量分數最小.


科目:高中數學 來源: 題型:
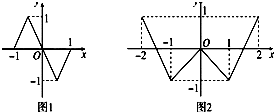 (2012•唐山二模)奇函數f(x)、偶函數g(x)的圖象分別如圖1、2所示,方程f(g(x))=0、g(f(x))=0的實根個數分別為a、b,則a+b=( )
(2012•唐山二模)奇函數f(x)、偶函數g(x)的圖象分別如圖1、2所示,方程f(g(x))=0、g(f(x))=0的實根個數分別為a、b,則a+b=( )查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•海淀區二模)如圖1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿對角線AC折起到△PAC的位置,如圖2所示,使得點P在平面ABC上的正投影H恰好落在線段AC上,連接PB,點E,F分別為線段PA,PB的中點.
(2013•海淀區二模)如圖1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿對角線AC折起到△PAC的位置,如圖2所示,使得點P在平面ABC上的正投影H恰好落在線段AC上,連接PB,點E,F分別為線段PA,PB的中點.查看答案和解析>>
科目:高中數學 來源:2014屆湖北省高三10月統一階段性考試理科數學試卷(解析版) 題型:選擇題
奇函數 、偶函數
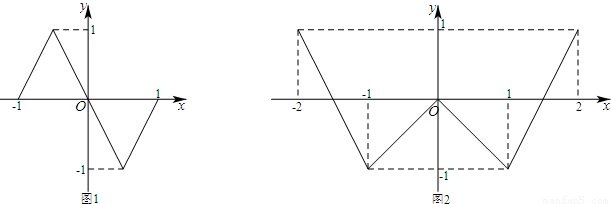
、偶函數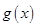 的圖象分別如圖1、2所示,方程
的圖象分別如圖1、2所示,方程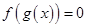 ,
,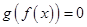 的實根個數分別為
的實根個數分別為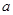 、
、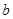 ,則
,則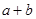 等于( )
等于( )
A. B.
B.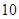 C.
C.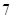 D.
D.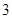
查看答案和解析>>
科目:高中數學 來源:2014屆江西省高三年級聯考理科數學試卷(解析版) 題型:選擇題
奇函數f(x)、偶函數g(x)的圖像分別如圖1、2所示,方程f(g(x))=0,g(f(x))=0的實根個數分別為a、b,則a+b= ( )

A. 14 B. 8 C. 7 D. 3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com