
分析 (1)利用導數的正負,即可證明;
(2)求出g(x)=x+$\frac{4}{x}$,又g(x)的定義域為(-∞,0)∪(0,+∞)關于原點對稱,利用奇函數的定義進行判斷;
(3)由(2)知f(x)=m可化為x+$\frac{4}{x}$=m-4(m≥8),再分類討論,即可得出結論.
解答 證明:(1)由題意:f(x)=x+$\frac{4}{x}$+a,
∴f′(x)=$\frac{{x}^{2}-4}{{x}^{2}}$,
∴0<x<2時,f′(x)<0,x>2時,f′(x)>0,
∴函數f(x)在(0,2]上是減函數,(2,+∞)上是增函數 …(4分)
解:(2)由題意知方程x2+ax+4=0有且只有一個實數根
∴△=a2-16=0,
又a>0,∴a=4.…(5分)
此時f(x)=x+$\frac{4}{x}$+4,g(x)=x+$\frac{4}{x}$,
又g(x)的定義域為(-∞,0)∪(0,+∞)關于原點對稱,…(6分)
且g(-x)=-x-$\frac{4}{x}$=-g(x),…(7分)
∴g(x)是奇函數 …(8分)
(3)由(2)知f(x)=m可化為x+$\frac{4}{x}$=m-4(m≥8)…(9分)
又由(1)(2)知:
當m-4=4 即m=8時f(x)=m只有一解 …(10分)
當m-4>4即m>8時f(x)=m有兩解 …(11分)
綜上,當m=8時f(x)=m只有一解;當m>8時f(x)=m有兩解; …(12分)
點評 本題考查函數的單調性與奇偶性,考查方程解的個數的判斷,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | [2,+∞) | B. | (-∞,-1] | C. | (-∞,-1]∪[2,+∞) | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
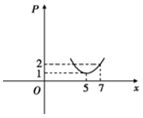 某產品關稅與市場供應量P的關系近似地滿足:P(x)=2${\;}^{(1-kt){{(x-b)}{\;}^2}}}$(其中t為關稅的稅率,且t∈[0,$\frac{1}{2}}$],x為市場價格,b,k為正常數),當t=$\frac{1}{8}$時,市場供應量曲線如圖所示:
某產品關稅與市場供應量P的關系近似地滿足:P(x)=2${\;}^{(1-kt){{(x-b)}{\;}^2}}}$(其中t為關稅的稅率,且t∈[0,$\frac{1}{2}}$],x為市場價格,b,k為正常數),當t=$\frac{1}{8}$時,市場供應量曲線如圖所示:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $y=\frac{1}{x}$ | B. | y=1g|x| | C. | y=cosx | D. | y=x2+2x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com