
已知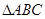 的兩個(gè)頂點(diǎn)
的兩個(gè)頂點(diǎn)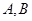 的坐標(biāo)分別
的坐標(biāo)分別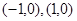 ,且
,且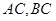 所在直線的斜率之積為
所在直線的斜率之積為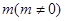 ,1)求頂點(diǎn)
,1)求頂點(diǎn) 的軌跡.2)當(dāng)
的軌跡.2)當(dāng)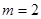 時(shí),記頂點(diǎn)
時(shí),記頂點(diǎn) 的軌跡為
的軌跡為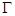 ,過(guò)點(diǎn)
,過(guò)點(diǎn)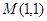 能否存在一條直線
能否存在一條直線 ,使
,使 與曲線
與曲線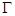 交于
交于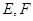 兩點(diǎn),且
兩點(diǎn),且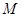 為線段
為線段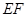 的中點(diǎn),若存在求直線
的中點(diǎn),若存在求直線 的方程,若不存在說(shuō)明理由.(12分)
的方程,若不存在說(shuō)明理由.(12分)
 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:2010-2011年廣東省廣州市高二下學(xué)期期末教學(xué)質(zhì)量檢測(cè)理科數(shù)學(xué) 題型:解答題
(本小題滿分12分)
已知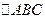 的兩個(gè)頂點(diǎn)
的兩個(gè)頂點(diǎn)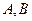 的坐標(biāo)為
的坐標(biāo)為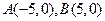 ,且
,且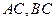 的斜率之積等于
的斜率之積等于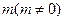 ,若頂點(diǎn)
,若頂點(diǎn)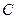 的軌跡是雙曲線(去掉兩個(gè)頂點(diǎn)),求
的軌跡是雙曲線(去掉兩個(gè)頂點(diǎn)),求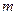 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2012-2013學(xué)年湖北省八市高三三月調(diào)考理科數(shù)學(xué)試卷(解析版) 題型:解答題
已知△ 的兩個(gè)頂點(diǎn)
的兩個(gè)頂點(diǎn)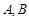 的坐標(biāo)分別是
的坐標(biāo)分別是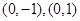 ,且
,且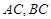 所在直線的斜率之積等于
所在直線的斜率之積等于 .
.
(Ⅰ)求頂點(diǎn)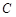 的軌跡
的軌跡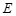 的方程,并判斷軌跡
的方程,并判斷軌跡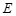 為何種圓錐曲線;
為何種圓錐曲線;
(Ⅱ)當(dāng) 時(shí),過(guò)點(diǎn)
時(shí),過(guò)點(diǎn)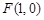 的直線
的直線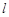 交曲線
交曲線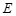 于
于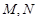 兩點(diǎn),設(shè)點(diǎn)
兩點(diǎn),設(shè)點(diǎn) 關(guān)于
關(guān)于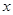 軸的對(duì)稱
軸的對(duì)稱
點(diǎn)為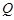 (
(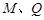 不重合) 試問(wèn):直線
不重合) 試問(wèn):直線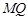 與
與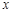 軸的交點(diǎn)是否是定點(diǎn)?若是,求出定點(diǎn),若不是,請(qǐng)說(shuō)明理由.
軸的交點(diǎn)是否是定點(diǎn)?若是,求出定點(diǎn),若不是,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2012-2013學(xué)年湖北省八市高三3月聯(lián)考理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分13分)已知△ 的兩個(gè)頂點(diǎn)
的兩個(gè)頂點(diǎn) 的坐標(biāo)分別是
的坐標(biāo)分別是 ,且
,且 所在直線的斜率之積等于
所在直線的斜率之積等于 .
.
(Ⅰ)求頂點(diǎn)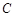 的軌跡
的軌跡 的方程,并判斷軌跡
的方程,并判斷軌跡 為何種圓錐曲線;
為何種圓錐曲線;
(Ⅱ)當(dāng) 時(shí),過(guò)點(diǎn)
時(shí),過(guò)點(diǎn) 的直線
的直線 交曲線
交曲線 于
于 兩點(diǎn),設(shè)點(diǎn)
兩點(diǎn),設(shè)點(diǎn) 關(guān)于
關(guān)于 軸的對(duì)稱點(diǎn)為
軸的對(duì)稱點(diǎn)為 (
( 不重合) 試問(wèn):直線
不重合) 試問(wèn):直線 與
與 軸的交點(diǎn)是否是定點(diǎn)?若是,求出定點(diǎn),若不是,請(qǐng)說(shuō)明理由.
軸的交點(diǎn)是否是定點(diǎn)?若是,求出定點(diǎn),若不是,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010年山西省高一上學(xué)期期中考試數(shù)學(xué)試卷 題型:解答題
已知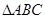 的兩個(gè)頂點(diǎn)
的兩個(gè)頂點(diǎn)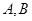 的坐標(biāo)分別
的坐標(biāo)分別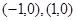 ,且
,且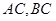 所在直線的斜率之積為
所在直線的斜率之積為 ,1)求頂點(diǎn)
,1)求頂點(diǎn)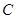 的軌跡.2)當(dāng)
的軌跡.2)當(dāng)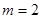 時(shí),記頂點(diǎn)
時(shí),記頂點(diǎn)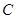 的軌跡為
的軌跡為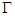 ,過(guò)點(diǎn)
,過(guò)點(diǎn)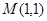 能否存在一條直線
能否存在一條直線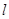 ,使
,使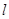 與曲線
與曲線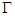 交于
交于 兩點(diǎn),且
兩點(diǎn),且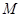 為線段
為線段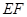 的中點(diǎn),若存在求直線
的中點(diǎn),若存在求直線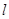 的方程,若不存在說(shuō)明理由.(12分)
的方程,若不存在說(shuō)明理由.(12分)
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com