
【題目】已知冪函數f(x)=xa的圖象經過點![]() .
.
(1)求函數f(x)的解析式,并判斷奇偶性;
(2)判斷函數f(x)在(﹣![]() ,0)上的單調性,并用單調性定義證明.
,0)上的單調性,并用單調性定義證明.
(3)作出函數f(x)在定義域內的大致圖象(不必寫出作圖過程).
科目:高中數學 來源: 題型:
【題目】已知函數 f(x)=asinx﹣bcosx(a,b為常數,a≠0,x∈R)在x= ![]() 處取得最小值,則函數g(x)=f(
處取得最小值,則函數g(x)=f( ![]() ﹣x)是( )
﹣x)是( )
A.偶函數且它的圖象關于點(π,0)對稱
B.奇函數且它的圖象關于點(π,0)對稱
C.奇函數且它的圖象關于點( ![]() ,0)對稱
,0)對稱
D.偶函數且它的圖象關于點( ![]() ,0)對稱
,0)對稱
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a∈R,函數f(x)滿足f(2x)=x2﹣2ax+a2﹣1.
(Ⅰ)求f(x)的解析式,并寫出f(x)的定義域;
(Ⅱ)若f(x)在 ![]() 上的值域為[﹣1,0],求實數a的取值范圍.
上的值域為[﹣1,0],求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,∠ABC= ![]() ,邊BC在平面α內,頂點A在平面α外,直線AB與平面α所成角為θ.若平面ABC與平面α所成的二面角為
,邊BC在平面α內,頂點A在平面α外,直線AB與平面α所成角為θ.若平面ABC與平面α所成的二面角為 ![]() ,則sinθ= .
,則sinθ= . 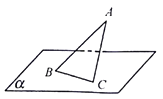
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= ![]() ,g(x)=a(x+b)(0<a≤1,b≤0).
,g(x)=a(x+b)(0<a≤1,b≤0).
(1)討論函數y=f(x)g(x)的奇偶性;
(2)當b=0時,判斷函數y= ![]() 在(﹣1,1)上的單調性,并說明理由;
在(﹣1,1)上的單調性,并說明理由;
(3)設h(x)=|af2(x)﹣ ![]() |,若h(x)的最大值為2,求a+b的取值范圍.
|,若h(x)的最大值為2,求a+b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘人常用小石子在沙灘上擺成各種形狀來研究數.比如:他們研究過圖(1)中的1,3,6,10,…,由于這些數能夠表示成三角形,所以將其稱為三角形數;類似地,稱圖(2)中的1,4,9,16,…這樣的數為正方形數.下列數中既是三角形數又是正方形數的是( )


A. 289 B. 1 024
C. 1 225 D. 1 378
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人從1,2,…,15這15個數中,依次任取一個數(不放回).則在已知甲取到的數是5的倍數的情況下,甲所取的數大于乙所取的數的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的偶函數,且在區間[0,+∞)上單調遞減,若f(log2a)+f(3 ![]() a)≥2f(﹣1),則實數a的取值范圍是( )
a)≥2f(﹣1),則實數a的取值范圍是( )
A.[2,4]
B.[ ![]() ,2]
,2]
C.[ ![]() ,4]
,4]
D.[ ![]() ,2]
,2]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線y=﹣x+1與橢圓 ![]() +
+ ![]() =1(a>b>0)相交于A、B兩點.
=1(a>b>0)相交于A、B兩點.
(1)若橢圓的離心率為 ![]() ,焦距為2,求線段AB的長;
,焦距為2,求線段AB的長;
(2)若向量 ![]() 與向量
與向量 ![]() 互相垂直(其中O為坐標原點),當橢圓的離心率e∈[
互相垂直(其中O為坐標原點),當橢圓的離心率e∈[ ![]() ,
, ![]() ]時,求橢圓的長軸長的最大值.
]時,求橢圓的長軸長的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com