
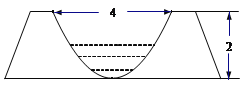
【題目】為響應新農村建設,某村計劃對現有舊水渠進行改造,已知舊水渠的橫斷面是一段拋物線弧,頂點為水渠最底端(如圖),渠寬為4m,渠深為2m.
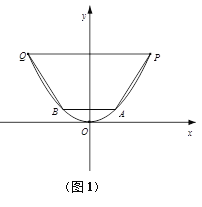
(1)考慮到農村耕地面積的減少,為節約水資源,要減少水渠的過水量,在原水渠內填土,使其成為橫斷面為等腰梯形的新水渠(如圖(1)建立平面直角坐標系),新水渠底面與地面平行(不改變渠寬),問新水渠底寬為多少時,所填土的土方量最少?
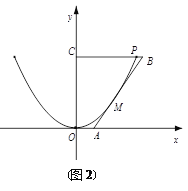
(2)考慮到新建果園的灌溉需求,要增大水渠的過水量,現把舊水渠改挖(不能填土)成橫斷面為等腰梯形的新水渠(如圖(2)建立平面直角坐標系),使水渠的底面與地面平行(不改變渠深),要使所挖土的土方量最少,請你設計水渠改挖后的底寬,并求出這個底寬.
【答案】(1)![]() ;(2)改挖后的水渠的底寬為
;(2)改挖后的水渠的底寬為![]() 時,可使挖土的土方量最少
時,可使挖土的土方量最少
【解析】試題分析:(1)建立坐標系,設拋物線的方程為![]() ,由已知點
,由已知點![]() 在拋物線上,推導出拋物線的方程,可得梯形
在拋物線上,推導出拋物線的方程,可得梯形![]() 面積,利用導數可得結論;(2)為了使挖掉的土最少,等腰梯形的兩腰必須與拋物線相切,設切點
面積,利用導數可得結論;(2)為了使挖掉的土最少,等腰梯形的兩腰必須與拋物線相切,設切點![]() ,則函數在點
,則函數在點![]() 的切線方程為
的切線方程為![]() ,由此能推導出設計改挖后的水渠的底寬為
,由此能推導出設計改挖后的水渠的底寬為![]() 時,可使用權所挖土的土方星最少.
時,可使用權所挖土的土方星最少.
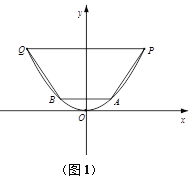
試題解析:建立如圖所示的直角坐標系,
設拋物線的方程為![]() ,由已知點
,由已知點![]() 在拋物線上,得
在拋物線上,得![]() ,所以拋物線的方程為
,所以拋物線的方程為![]() .
.
(1)為了使填入的土最少,內接等腰梯形的面積要最大,如圖1,設點![]() ,則此時梯形APQB的面積
,則此時梯形APQB的面積![]() ,
,
∴![]() ,令
,令![]() ,得
,得![]() ,
,
當![]() 時,
時, ![]() ,
, ![]() 單調遞增,當
單調遞增,當![]() 時,
時, ![]() ,
, ![]() 單調遞減,
單調遞減,
所以當![]() 時,
時, ![]() 有最大值
有最大值![]() ,改挖后的水渠的底寬為
,改挖后的水渠的底寬為![]() m時,可使填土的土方量最少.
m時,可使填土的土方量最少.
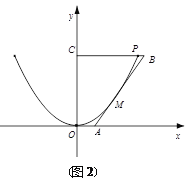
(2)為了使挖掉的土最少,等腰梯形的兩腰必須與拋物線相切,如圖2,設切點![]() ,則函數在點M處的切線方程為
,則函數在點M處的切線方程為![]() ,分別令
,分別令![]() 得
得![]() ,所以此時梯形OABC的面積
,所以此時梯形OABC的面積![]() ,當且僅當
,當且僅當![]() 時,等號成立,此時
時,等號成立,此時![]() .所以設計改挖后的水渠的底寬為
.所以設計改挖后的水渠的底寬為![]() m時,可使挖土的土方量最少.
m時,可使挖土的土方量最少.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】若實數數列![]() 滿足
滿足![]() ,則稱數列
,則稱數列![]() 為“
為“![]() 數列”.
數列”.
(Ⅰ)若數列![]() 是
是![]() 數列,且
數列,且![]() ,求
,求![]() ,
,![]() 的值;
的值;
(Ⅱ)求證:若數列![]() 是
是![]() 數列,則
數列,則![]() 的項不可能全是正數,也不可能全是負數;
的項不可能全是正數,也不可能全是負數;
(Ⅲ)若數列![]() 為
為![]() 數列,且
數列,且![]() 中不含值為零的項,記
中不含值為零的項,記![]() 前
前![]() 項中值為負數的項的個數為
項中值為負數的項的個數為![]() ,求
,求![]() 所有可能取值.
所有可能取值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,函數
,函數![]() 的導函數為
的導函數為![]() .
.
⑴ 若直線![]() 與曲線
與曲線![]() 恒相切于同一定點,求
恒相切于同一定點,求![]() 的方程;
的方程;
⑵ 若![]() ,求證:當
,求證:當![]() 時,
時, ![]() 恒成立;
恒成立;
⑶ 若當![]() 時,
時, ![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解春季晝夜溫差大小與某種子發芽多少之間的關系,現在從4月份的30天中隨機挑選了5天進行研究,且分別記錄了每天晝夜溫差與每天100顆種子浸泡后的發芽率,得到如下表格:

(1)從這5天中任選2天,記發芽的種子數分別為![]() ,求事件“
,求事件“![]() 均不小于25” 的概率;
均不小于25” 的概率;
(2)從這5天中任選2天,若選取的是4月1日與4月30日的兩組數據,請根據這5天中的另3天的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2顆,則認為得到的線性回歸方程是可靠的,試問(2)中所得到的線性回歸方程是否可靠?
參考公式: 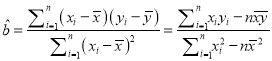 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=(1+x)m+(1+2x)n(m,n∈N*)的展開式中x的系數為11.
(1)求x2的系數取最小值時n的值;
(2)當x2的系數取得最小值時,求f(x)展開式中x的奇次冪項的系數之和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,若橢圓經過點
,若橢圓經過點![]() ,且
,且![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設斜率為![]() 的直線
的直線![]() 與以原點為圓心,半徑為
與以原點為圓心,半徑為![]() 的圓交于
的圓交于![]() ,
,![]() 兩點,與橢圓
兩點,與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,當
,當![]() 取得最小值時,求直線
取得最小值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量x(噸)與相應的生產能耗y(噸標準煤)的幾組對照數據.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程![]() ;
;
(3)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據(2)求出的線性回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤.
(參考數值:3×2.5+4×3+5×4+6×4.5=66.5)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com