
 .
. ,
, (3分)
(3分) (6分),
(6分), .
. ,所以
,所以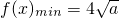 (8分),
(8分), .(14分)
.(14分) ,即可得到
,即可得到 ,再利用一元二次不等式的解法得到答案.
,再利用一元二次不等式的解法得到答案.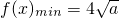 ,所以由f(x)>b2恒成立可得16a>b4.首先計算出基本事件總數,再利用列舉的方法得到此事件包含的基本事件,進而根據等可能事件的概率公式得到答案.
,所以由f(x)>b2恒成立可得16a>b4.首先計算出基本事件總數,再利用列舉的方法得到此事件包含的基本事件,進而根據等可能事件的概率公式得到答案.

 名校課堂系列答案
名校課堂系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com