【題目】橢圓
＋
＝1(a>b>0)的一個焦點為F1，若橢圓上存在一個點P，滿足以橢圓短軸為直徑的圓與線段PF1相切于該線段的中點，則橢圓的離心率為________．
期末100分闖關海淀考王系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝sinxcosx
cos2x+1
（1）求f（x）的最小正周期和最大值，并寫出取得最大值時x的集合；
（2）將f（x）的函數圖象向左平移φ（φ＞0）個單位后得到的函數g（x）是偶函數，求φ的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓O經過橢圓C：
=1（a＞b＞0）的兩個焦點以及兩個頂點，且點（b，
）在橢圓C上．
（Ⅰ）求橢圓C的方程；
（Ⅱ）若直線l與圓O相切，與橢圓C交于M、N兩點，且|MN|=
，求直線l的傾斜角．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
的右頂點為A，上頂點為B．已知橢圓的離心率為
，
．
（1）求橢圓的方程；
（2）設直線
與橢圓交于
，
兩點，
與直線
交于點M，且點P，M均在第四象限．若
的面積是
面積的2倍，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數f（x），若f（x0）＝x0，則稱x0為f（x）的不動點.設f（x）＝x3+ax2+bx+3.
（1）當a＝0時，
（i）求f（x）的極值點；
（ⅱ）若存在x0既是f（x）的極值點，也是f（x）的不動點，求b的值；
（2）是否存在a，b，使得f（x）有兩個極值點，且這兩個極值點均為f（x）的不動點？說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
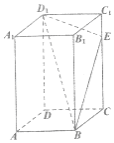
【題目】如圖，已知在長方體
中，
，
，
，點
為
上的一個動點，平面
與棱
交于點
，給出下列命題：
①四棱錐
的體積為20；
②存在唯一的點，使截面四邊形
的周長取得最小值
；
③當點不與
，
重合時，在棱
上均存在點
，使得
平面；
④存在唯一的點，使得
平面，且
．
其中正確的命題是_____（填寫所有正確的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
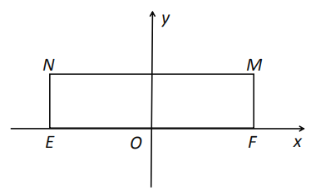
【題目】已知矩形EFMN，
，
，以EF的中點O為原點，建立如圖的平面直角坐標系，若橢圓
以E，F為焦點，且經過M，N兩點.
（1）求橢圓的方程；
（2）直線
與相交于A，B兩點，在y軸上是否存在點C，使得△ABC為正三角形，若存在，求出l的方程；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著經濟的發展，城市空氣質量也越來越引起了人民的關注，如圖是我國某大城市2018年1月至8月份的空氣質量檢測結果，圖中一、二、三、四級是空氣質量等級，一級空氣質量最好，一級和二級都是空氣質量合格，下面說法錯誤的是（ ）
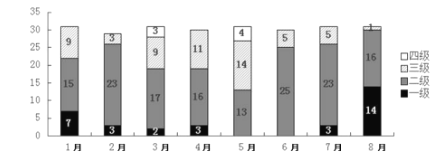
A.6月的空氣質量最差
B.8月是空氣質量最好的一個月
C.第二季度與第一季度相比，空氣質量合格天數的比重下降了
D.1月至8月空氣質量合格天數超過20天的月份有5個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定點
，
，直線
、
相交于點
，且它們的斜率之積為
，記動點的軌跡為曲線
。
（1）求曲線的方程；
（2）過點
的直線與曲線交于
、
兩點，是否存在定點
，使得直線
與
斜率之積為定值，若存在，求出
坐標；若不存在，請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
