Question

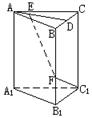
如圖：已知直三棱柱ABC—A₁B₁C₁，AB＝AC，F為棱BB₁上一點，BF∶FB₁＝2∶1，BF＝BC＝2a。

　　（I）若D為BC的中點，E為AD上不同于A、D的任意一點，證明EF⊥FC₁；

　　（II）試問：若AB＝2a，在線段AD上的E點能否使EF與平面BB₁C₁C成60°角，為什么？證明你的結論

Answer 1

（Ⅰ）證明見解析（Ⅱ）60°

解析:

（I）連結DF，DC 　∵三棱柱ABC—A₁B₁C₁是直三棱柱，

　　∴CC₁⊥平面ABC，∴平面BB₁C₁C⊥平面ABC

　　∵AB＝AC，D為BC的中點，∴AD⊥BC，AD⊥平面BB₁C₁C                                             3＇

　　∴DF為EF在平面BB₁C₁C上的射影，

　　在△DFC₁中，∵DF²＝BF²＋BD²＝5a²，＝＋DC²＝10a²，

　　＝B₁F²＋＝5a²，　∴＝DF²＋，∴DF⊥FC₁

FC₁⊥EF                                                                

　　（II）∵AD⊥平面BB₁C₁C，∴∠DFE是EF與平面BB₁C₁C所成的角                                    

　　在△EDF中，若∠EFD＝60°，則ED＝DFtg60°＝·＝，

　　∴＞，∴E在DA的延長線上，而不在線段AD上                                

　　故線段AD上的E點不能使EF與平面BB₁C₁C成60°角。