
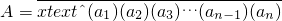 .如:
.如: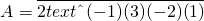 ,則表示A是一個2進制形式的數,且A=-1+3×2+(-2)×22+1×23=5.
,則表示A是一個2進制形式的數,且A=-1+3×2+(-2)×22+1×23=5.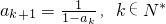 ,
,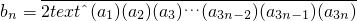 (n∈N*),是否存在實常數p和q,對于任意的n∈N*,bn=p•8n+q總成立?若存在,求出p和q;若不存在,說明理由.
(n∈N*),是否存在實常數p和q,對于任意的n∈N*,bn=p•8n+q總成立?若存在,求出p和q;若不存在,說明理由.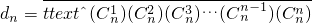 ,求
,求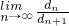 .
.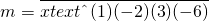
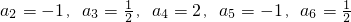
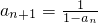 ∴
∴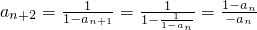
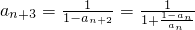 =an(n∈N*),知{an}是周期為3的數列
=an(n∈N*),知{an}是周期為3的數列 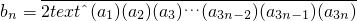
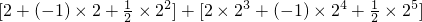
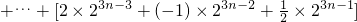 =
=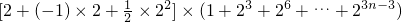 =
=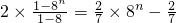
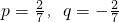 .
.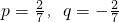 ,對于任意的n∈N*,
,對于任意的n∈N*,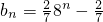 總成立
總成立 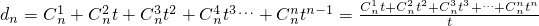 =
=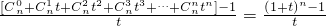
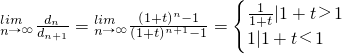 ,即
,即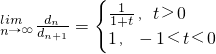
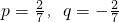 .
.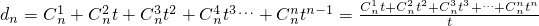 =
=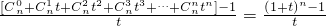 ,再求極限.
,再求極限.

 寒假學與練系列答案
寒假學與練系列答案科目:高中數學 來源: 題型:
. |
| x\~(a1)(a2)(a3)…(an-1)(an) |
. |
| 2\~(-1)(3)(-2)(1) |
| 1 |
| 1-ak |
. |
| 2\~(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
. | ||||||||||
t\~(
|
| lim |
| n→∞ |
| dn |
| dn+1 |
查看答案和解析>>
科目:高中數學 來源:2008-2009學年度高三數學模擬試題分類匯編:數列 題型:044
我們規定:對于任意實數A,若存在數列{an}和實數x(x≠0),使得A=a1+a2x+a3x2+…+anxn-1,則稱數A可以表示成x進制形式,簡記為:
![]() .如:
.如:![]() ,則表示A是一個2進制形式的數,且A=-1+3×2+(-2)×22+1×23=5.
,則表示A是一個2進制形式的數,且A=-1+3×2+(-2)×22+1×23=5.
(1)已知m=(1-2x)(1+3x2)(其中x≠0),試將m表示成x進制的簡記形式.
(2)若數列{an}滿足a1=2,![]() ,
,
![]()
![]() ,是否存在實常數p和q,對于任意的n∈N*,bn=p·8n+q總成立?若存在,求出p和q;若不存在,說明理由.
,是否存在實常數p和q,對于任意的n∈N*,bn=p·8n+q總成立?若存在,求出p和q;若不存在,說明理由.
(3)若常數t滿足t≠0且t>-1,![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源:奉賢區模擬 題型:解答題
| . |
| x\~(a1)(a2)(a3)…(an-1)(an) |
| . |
| 2\~(-1)(3)(-2)(1) |
| 1 |
| 1-ak |
| . |
| 2\~(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
| . | ||||||||||
t\~(
|
| lim |
| n→∞ |
| dn |
| dn+1 |
查看答案和解析>>
科目:高中數學 來源:2008年上海市奉賢區高三聯考數學試卷(理科)(解析版) 題型:解答題
 .如:
.如: ,則表示A是一個2進制形式的數,且A=-1+3×2+(-2)×22+1×23=5.
,則表示A是一個2進制形式的數,且A=-1+3×2+(-2)×22+1×23=5. ,
, (n∈N*),是否存在實常數p和q,對于任意的n∈N*,bn=p•8n+q總成立?若存在,求出p和q;若不存在,說明理由.
(n∈N*),是否存在實常數p和q,對于任意的n∈N*,bn=p•8n+q總成立?若存在,求出p和q;若不存在,說明理由. ,求
,求 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com