
【題目】如圖,在三棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為線段
分別為線段![]() ,
,![]() 上的點(diǎn),且
上的點(diǎn),且![]() ,
,![]() .
.
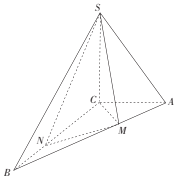
(1)證明:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見(jiàn)證明;(2)![]()
【解析】
(1)證明BC⊥平面SAC,即可推出SC⊥平面ABC,從而得到MN⊥平面SCM,即可證明MN⊥SM.(2)以C為原點(diǎn),以![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向建立空間直角坐標(biāo)系
軸的正方向建立空間直角坐標(biāo)系![]() ,求出平面SAM和平面SMN的法向量,利用空間向量的夾角的余弦,求解二面角A﹣SM﹣N的余弦值.
,求出平面SAM和平面SMN的法向量,利用空間向量的夾角的余弦,求解二面角A﹣SM﹣N的余弦值.
(1)證明:由![]() ,
,![]() ,且
,且![]() ,則
,則![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() ,又
,又![]() ,
,![]() ,則
,則![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() .
.
因?yàn)?/span>![]() ,
,![]() ,所以
,所以![]() ,故
,故![]() .
.
又因?yàn)?/span>![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,則
,則![]() .
.
(2)解:由(1)知,![]() ,
,![]() ,
,![]() 兩兩相互垂直,
兩兩相互垂直,
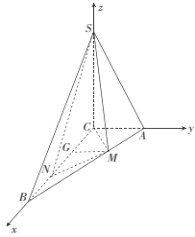
如圖是以![]() 為坐標(biāo)原點(diǎn),分別以
為坐標(biāo)原點(diǎn),分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向建立空間直角坐標(biāo)系
軸的正方向建立空間直角坐標(biāo)系![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則
![]() ,令
,令![]() ,得
,得![]() .
.
設(shè)平面![]() 的法向量為
的法向量為![]() ,
,
則![]() ,令
,令![]() ,則
,則![]() ,
,![]() ,故
,故![]() .
.
所以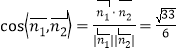 ,
,
由圖可知二面角![]() 為鈍角,
為鈍角,
故二面角![]() 的余弦值為
的余弦值為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
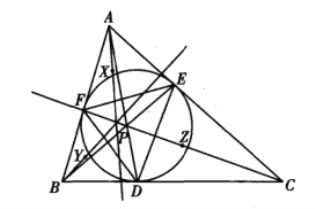
【題目】如圖,△ABC的內(nèi)切圓分別與邊BC、CA、AB切于點(diǎn)D、E、F,AD與BE交于點(diǎn)P,設(shè)點(diǎn)P關(guān)于直線EF、FD、DE的對(duì)稱點(diǎn)分別X、Y、Z.證明:AX、BY、CZ三線共點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若非負(fù)整數(shù)m、n在求和時(shí)恰進(jìn)位一次(十進(jìn)制下),則稱有序數(shù)對(duì)(m、n)為“好的”,那么,所有和為2014的好的有序數(shù)對(duì)的個(gè)數(shù)為__________。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=lnx![]() ,其中a>0.曲線y=f(x)在點(diǎn)(1,f(1))處的切線與直線y=x+1垂直.
,其中a>0.曲線y=f(x)在點(diǎn)(1,f(1))處的切線與直線y=x+1垂直.
(1)求函數(shù)f(x)的單調(diào)區(qū)間;
(2)求函數(shù)f(x)在區(qū)間[1,e]上的極值和最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)![]() ,拋物線
,拋物線![]() :
:![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,射線
,射線![]() 與拋物線
與拋物線![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,與其準(zhǔn)線相交于點(diǎn)
,與其準(zhǔn)線相交于點(diǎn)![]() ,則
,則![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
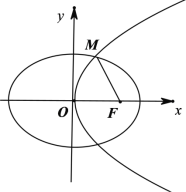
【題目】已知拋物線C:y2=4x與橢圓E:![]() 1(a>b>0)有一個(gè)公共焦點(diǎn)F.設(shè)拋物線C與橢圓E在第一象限的交點(diǎn)為M.滿足|MF|
1(a>b>0)有一個(gè)公共焦點(diǎn)F.設(shè)拋物線C與橢圓E在第一象限的交點(diǎn)為M.滿足|MF|![]() .
.
(1)求橢圓E的標(biāo)準(zhǔn)方程;
(2)過(guò)點(diǎn)P(1,![]() )的直線交拋物線C于A、B兩點(diǎn),直線PO交橢圓E于另一點(diǎn)Q.若P為AB的中點(diǎn),求△QAB的面積.
)的直線交拋物線C于A、B兩點(diǎn),直線PO交橢圓E于另一點(diǎn)Q.若P為AB的中點(diǎn),求△QAB的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】橢圓![]() 的離心率是
的離心率是![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 做斜率為
做斜率為![]() 的直線
的直線![]() ,橢圓
,橢圓![]() 與直線
與直線![]() 交于
交于![]() 兩點(diǎn),當(dāng)直線
兩點(diǎn),當(dāng)直線![]() 垂直于
垂直于![]() 軸時(shí)
軸時(shí)![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)當(dāng)![]() 變化時(shí),在
變化時(shí),在![]() 軸上是否存在點(diǎn)
軸上是否存在點(diǎn)![]() ,使得
,使得![]() 是以
是以![]() 為底的等腰三角形,若存在求出
為底的等腰三角形,若存在求出![]() 的取值范圍,若不存在說(shuō)明理由.
的取值范圍,若不存在說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() ,三角形
,三角形![]() 的兩條邊
的兩條邊![]() 所在直線的斜率之積是
所在直線的斜率之積是![]() .
.
(I)求點(diǎn)![]() 的軌跡方程;
的軌跡方程;
(II)設(shè)直線![]() 方程為
方程為![]() ,直線
,直線![]() 方程為
方程為![]() ,直線
,直線![]() 交
交![]() 于
于![]() ,點(diǎn)
,點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸對(duì)稱,直線
軸對(duì)稱,直線![]() 與
與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() ,求
,求![]() 面積
面積![]() 關(guān)于
關(guān)于![]() 的表達(dá)式.
的表達(dá)式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】現(xiàn)對(duì)某市工薪階層關(guān)于“樓市限購(gòu)令”的態(tài)度進(jìn)行調(diào)查,隨機(jī)抽調(diào)了50人,他們?cè)率杖氲念l數(shù)分布及對(duì)“樓市限購(gòu)令”贊成人數(shù)如下表.
月收入(單位百元) |
|
|
|
|
|
|
頻數(shù) | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數(shù) | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上統(tǒng)計(jì)數(shù)據(jù)填下面2×2列聯(lián)表,并問(wèn)是否有99%的把握認(rèn)為“月收入以5500元為分界點(diǎn)對(duì)“樓市限購(gòu)令”的態(tài)度有差異;
月收入不低于55百元的人數(shù) | 月收入低于55百元的人數(shù) | 合計(jì) | |
贊成 | a=______________ | c=______________ | ______________ |
不贊成 | b=______________ | d=______________ | ______________ |
合計(jì) | ______________ | ______________ | ______________ |
(2)試求從年收入位于![]() (單位:百元)的區(qū)間段的被調(diào)查者中隨機(jī)抽取2人,恰有1位是贊成者的概率。
(單位:百元)的區(qū)間段的被調(diào)查者中隨機(jī)抽取2人,恰有1位是贊成者的概率。
參考公式: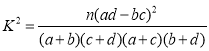 ,其中
,其中![]() .
.
參考值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com