
某商店試銷某種商品,獲得如下數據:
| 日銷售量(件) | 0 | 1 | 2 | 3 |
| 概率 | 0.05 | 0.25 | 0.45 | 0.25 |
(1)0.3 ,(2)X的分布列為X 2 3 4 P 0.25 0.3 0.45
期望EX=3.2
解析試題分析:(1)即指當天出售的件數少于2件 2分 概率P=0.05+0.25=0.3 3分
概率P=0.05+0.25=0.3 3分
(2)X的可能取值為2,3,4 6分
X=2指當天只出售1件,則P(X=2)=0.25
X=3指當天出售0件或3件,則P(X=3)=0.05+0.25=0.3
X=4指當天出售2件,則P(X=4)=0.45 9分 X的分布列為
X的分布列為X 2 3 4 P 0.25 0.3 0.45
期望EX=2×0.25+3×0.3+4×0.45=3.2 12分
考點:本題考查了概率與統計
點評:在求概率時,應注意立事件概率公式的應用,還有區分是屬于什么事件.求分布列時要掌握分布列的概念及性質


科目:高中數學 來源: 題型:解答題
“肇實,正名芡實,因肇慶所產之芡實顆粒大、藥力強,故名。”某科研所為進一步改良肇實,為此對肇實的兩個品種(分別稱為品種A和品種B)進行試驗.選取兩大片水塘,每大片水塘分成n小片水塘,在總共2n小片水塘中,隨機選n小片水塘種植品種A,另外n小片水塘種植B.
(1)假設n=4,在第一大片水塘中,種植品種A的小片水塘的數目記為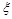 ,求
,求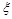 的分布列和數學期望;
的分布列和數學期望;
(2)試驗時每大片水塘分成8小片,即n=8,試驗結束后得到品種A和品種B在每個小片水塘上的每畝產量(單位:kg/畝)如下表:
| 號碼 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 品種A | 101 | 97 | 92 | 103 | 91 | 100 | 110 | 106 |
| 品種B | 115 | 107 | 112 | 108 | 111 | 120 | 110 | 113 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
袋中裝有大小相同的2個白球和3個黑球.
(1)采取放回抽樣方式,從中依次摸出兩個球,求兩球顏色不同的概率;
(2)采取不放回抽樣方式,從中依次摸出兩個球,記 為摸出兩球中白球的個數,
為摸出兩球中白球的個數,
求 的期望.
的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
三人獨立破譯同一密碼,已知三人各自破譯出密碼的概率分別為 ,且他們是否譯出密碼互不影響。
,且他們是否譯出密碼互不影響。
(1)求恰有兩人破譯出密碼的概率;
(2)“密碼被破譯”與“密碼未被破譯”的概率那個大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙、丙三人獨立破譯同一份密碼,已知甲、乙、丙各自破譯出密碼的概率分別為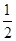 、
、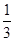 、
、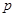 ,且他們是否破譯出密碼互不影響,若三人中只有甲破譯出密碼的概率為
,且他們是否破譯出密碼互不影響,若三人中只有甲破譯出密碼的概率為 .
.
(1)求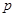 的值.
的值.
(2)設甲、乙、丙三人中破譯出密碼的人數為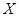 ,求
,求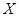 的分布列和數學期望
的分布列和數學期望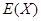 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了防止受污染的產品影響我國民眾的身體健康,要求產品在進入市場前必須進行兩輪檢測,只有兩輪都合格才能進行銷售,否則不能銷售.已知某產品第一輪檢測不合格的概率為 ,第二輪檢測不合格的概率為
,第二輪檢測不合格的概率為 ,兩輪檢測是否合格相互沒有影響.
,兩輪檢測是否合格相互沒有影響.
(Ⅰ)求該產品不能銷售的概率;
(Ⅱ)如果產品可以銷售,則每件產品可獲利40元;如果產品不能銷售,則每件產品虧損80元(即獲利-80元).已知一箱中有產品4件,記一箱產品獲利X元,求X的分布列,并求出均值E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
“H7N9禽流感”問題越來越引起社會關注,我校對高一600名學生進行了一次“H7N9禽流感”知識測試,并從中抽取了部分學生的成績(滿分100分)作為樣本,繪制了下面尚未完成的頻率分布表和頻率分布直方圖.
(1)填寫答題卡頻率分布表中的空格,補全頻率分布直方圖,并標出每個小矩形對應的縱軸數據;
(2)試估計該年段成績在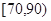 段的有多少人;
段的有多少人;
(3)請你估算該年級的平均分.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某廣場上有4盞裝飾燈,晚上每盞燈都隨機地閃爍紅燈或綠燈,每盞燈出現紅燈的概率都是 ,出現綠燈的概率都是
,出現綠燈的概率都是 .記這4盞燈中出現紅燈的數量為
.記這4盞燈中出現紅燈的數量為 ,當這排裝飾燈閃爍一次時:
,當這排裝飾燈閃爍一次時:
(1)求 時的概率;(2)求
時的概率;(2)求 的數學期望.
的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com