
【題目】(文)(2017·開封二模)為備戰某次運動會,某市體育局組建了一個由4個男運動員和2個女運動員組成的6人代表隊并進行備戰訓練.
(1)經過備戰訓練,從6人中隨機選出2人進行成果檢驗,求選出的2人中至少有1個女運動員的概率.
(2)檢驗結束后,甲、乙兩名運動員的成績用莖葉圖表示如圖:

計算說明哪位運動員的成績更穩定.
【答案】(1)![]() (2)乙
(2)乙
【解析】試題分析:(1)求出從6人中隨機選出2人,選出的2人中至少有1個女運動員的基本事件數,計算對應的概率值;
(2)根據題目中莖葉圖的數據,計算甲、乙運動員的平均成績與方差,比較大小即可得出結論.
試題解析:
(1)把4個男運動員和2個女運動員分別記為a1,a2,a3,a4和b1,b2.
則基本事件包括(a1,a2),(a1,a3),(a1,a4),(a1,b1),(a1,b2),(a2,a3),(a2,a4),(a2,b1),(a2,b2),(a3,a4),(a3,b1),(a3,b2),(a4,b1),(a4,b2),(b1,b2)共15種.
其中至少有1個女運動員的情況有9種,
故至少有1個女運動員的概率P=![]() =
=![]() .
.
(2)設甲運動員的平均成績為![]() 甲,方差為s
甲,方差為s![]() ,乙運動員的平均成績為
,乙運動員的平均成績為![]() 乙,方差為s
乙,方差為s![]() ,
,
可得![]() 甲=
甲=![]() =71,
=71,![]() 乙=
乙=![]() =71,
=71,
s![]() =
=![]() [(68-71)2+(70-71)2+(71-71)2+(72-71)2+(74-71)2]=4,
[(68-71)2+(70-71)2+(71-71)2+(72-71)2+(74-71)2]=4,
s![]() =
=![]() [(69-71)2+(70-71)2+(70-71)2+(72-71)2+(74-71)2]=3.2.
[(69-71)2+(70-71)2+(70-71)2+(72-71)2+(74-71)2]=3.2.
因為![]() 甲=
甲=![]() 乙,s
乙,s![]() >s
>s![]() ,故乙運動員的成績更穩定.
,故乙運動員的成績更穩定.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(1)若曲線![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 垂直,求實數
垂直,求實數![]() 的值;
的值;
(2)設![]() ,若對任意兩個不等的正數
,若對任意兩個不等的正數![]() ,都有
,都有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某校隨機抽取200名學生,獲得了他們一周課外閱讀時間(單位:h)的數據,整理得到數據的頻數分布表和頻率分布直方圖(如圖).
編 號 | 分 組 | 頻 數 |
1 | [0,2) | 12 |
2 | [2,4) | 16 |
3 | [4,6) | 34 |
4 | [6,8) | 44 |
續 表
編 號 | 分 組 | 頻 數 |
5 | [8,10) | 50 |
6 | [10,12) | 24 |
7 | [12,14) | 12 |
8 | [14,16) | 4 |
9 | [16,18] | 4 |
合計 | 200 |

(1)從該校隨機選取一名學生,試估計這名學生該周課外閱讀時間少于12 h的概率;
(2)求頻率分布直方圖中的a,b的值;
(3)假設同一組中的每個數據可用該組區間的中點值代替,試估計樣本中的200名學生該周課外閱讀時間的平均數在第幾組.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解《中華人民共和國道路交通安全法》在學生中的普及情況,調查部門對某校6名學生進行問卷調查,6人得分情況為:5,6,7,8,9,10.把這6名學生的得分看成一個總體.
(1)求該總體的平均數;
(2)用簡單隨機抽樣方法從這6名學生中抽取2名,他們的得分組成一個樣本.求該樣本平均數與總體平均數之差的絕對值不超過0.5的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·湖北武漢第二次調研)如圖是依據某城市年齡在20歲到45歲的居民上網情況調查而繪制的頻率分布直方圖,現已知年齡在[30,35),[35,40),[40,45)的上網人數呈現遞減的等差數列分布,則年齡在[35,40)的網民出現的頻率為 ( )
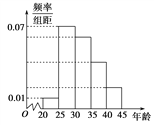
A. 0.04 B. 0.06
C. 0.2 D. 0.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(文)(2017·衡水二模)某商場在元旦舉行購物抽獎促銷活動,規定顧客從裝有編號0,1,2,3,4的五個相同小球的抽獎箱中一次任意摸出兩個小球,若取出的兩個小球的編號之和等于7則中一等獎,等于6或5則中二等獎,等于4則中三等獎,其余結果為不中獎.
(1)求中二等獎的概率.
(2)求不中獎的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在海岸![]() 處,發現北偏東
處,發現北偏東![]() 方向,距離
方向,距離![]() 為
為![]() 海里的
海里的![]() 處有一艘走私船,在
處有一艘走私船,在![]() 處北偏西
處北偏西![]() 方向,距離
方向,距離![]() 為
為![]() 海里的
海里的![]() 處有一艘緝私艇奉命以
處有一艘緝私艇奉命以![]() 海里/時的速度追截走私船,此時,走私船正以
海里/時的速度追截走私船,此時,走私船正以![]() 海里/時的速度從
海里/時的速度從![]() 處向北偏東
處向北偏東![]() 方向逃竄.
方向逃竄.
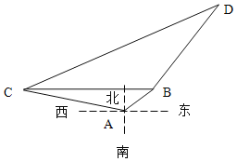
(1)問![]() 船與
船與![]() 船相距多少海里?
船相距多少海里?![]() 船在
船在![]() 船的什么方向?
船的什么方向?
(2)問緝私艇沿什么方向行駛才能最快追上走私船?并求出所需時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為: ![]() (
(![]() 為參數,
為參數, ![]() ),將曲線
),將曲線![]() 經過伸縮變換:
經過伸縮變換:  得到曲線
得到曲線![]() .
.
(1)以原點為極點, ![]() 軸的正半軸為極軸建立坐標系,求
軸的正半軸為極軸建立坐標系,求![]() 的極坐標方程;
的極坐標方程;
(2)若直線![]() (
(![]() 為參數)與
為參數)與![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產某種產品進行出售,當這種產品定價為每噸1000元時,每月可售出產品100噸.當每噸價格每增加20元時,月售出量將會減少1噸.產品每噸生產成本400元,月固定成本為20000元.
(Ⅰ)當產品每噸定價為1200元時,該公司月利潤是多少?
(Ⅱ)當產品每噸定價為多少元時,該公司的月利潤最大?最大月利潤是多少?(利潤=總收入-生產成本-固定成本)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com