Question

P是拋物線y²=x上的動點，Q是圓（x-3）²+y²=1的動點，則|PQ|的最小值為    ．

Answer 1

【答案】分析：設圓心為C，則|PQ|=|CP|-|CQ|=|CP|-1，將|PQ|的最小問題，轉化為|CP|的最小問題即可．
解答：解：設圓心為C，則|PQ|=|CP|-|CQ|=|CP|-1，C點坐標（3，0），
由于P在y²=x上，設P的坐標為（y²，y），
∴|CP|==
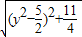
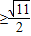
∵圓半徑為1，
所以|PQ|最小值為．
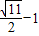
故答案為：．
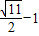
點評：本題重點考查圓與圓錐曲線的綜合，考查拋物線上的動點和圓上的動點間的距離的最小值，將|PQ|的最小問題，轉化為|CP|的最小問題是解題的關鍵．