
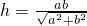 ;現在把結論類比到空間:三棱錐S-ABC的三條側棱SA,SB,SC兩兩相互垂直,SH⊥平面ABC,且SA=a,SB=b,SC=c,則點S到平面ABC的距離h'=________.
;現在把結論類比到空間:三棱錐S-ABC的三條側棱SA,SB,SC兩兩相互垂直,SH⊥平面ABC,且SA=a,SB=b,SC=c,則點S到平面ABC的距離h'=________.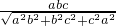
 ,SM=
,SM=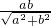 ,同理在直角三角形CSM中可求得|CM|=
,同理在直角三角形CSM中可求得|CM|=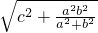 ,于是S△ABC=
,于是S△ABC= •|AB|•|CM|=
•|AB|•|CM|= •
• •
•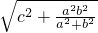 =
= •
•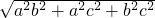 ,由VS-ABC=VC-ABS,即可求得S到平面ABC的距離為h′.
,由VS-ABC=VC-ABS,即可求得S到平面ABC的距離為h′.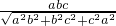 .
. ,又ab=|AB|•|SM|
,又ab=|AB|•|SM|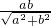 ,
,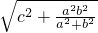 ,
, •|AB|•|CM|=
•|AB|•|CM|= •
• •
•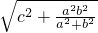 =
= •
•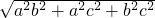 ,
, •
• abc=
abc= S△ABC•h′=
S△ABC•h′= •
• •
•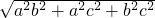 •h′,
•h′,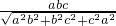 ,
,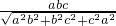 .
.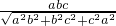 .
.

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com