
 ,
, 均為單位向量,若|
均為單位向量,若| +
+ |>1,則
|>1,則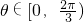
 ],且|x1|>|x2|時,有f(x1)>f(x2),
],且|x1|>|x2|時,有f(x1)>f(x2), 與
與 的夾角為θ,將已知等式平方,結合向量模的含義和單位向量長度為1,化簡整理可得
的夾角為θ,將已知等式平方,結合向量模的含義和單位向量長度為1,化簡整理可得 •
• =-
=- ,再結合向量數量積的定義和夾角的范圍,可得夾角θ的范圍.
,再結合向量數量積的定義和夾角的范圍,可得夾角θ的范圍. 與
與 的夾角為θ,
的夾角為θ, +
+ |>1,∴(
|>1,∴( +
+ )2=
)2= 2+2
2+2 •
• +
+ 2>1…(*)
2>1…(*) ,
, 均為單位向量,可得|
均為單位向量,可得| |=|
|=| |=1
|=1 •
• +1=1>1,所以
+1=1>1,所以 •
• >-
>-
 |•|
|•| |cosθ>-
|cosθ>-
 ,結合θ∈[0,π],得
,結合θ∈[0,π],得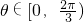 .①正確.
.①正確. ]上遞增,
]上遞增, =1,正確.
=1,正確.

 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com