【題目】已知直線
,直線
以及
上一點
.圓
的圓心在
上,且與直線相切于點
.
(1)求圓的方程;
(2)求過點
,被圓截得弦長為
的直線
的方程.
【答案】(1) 
;(2) 
或
【解析】
(1) 設圓心為
，半徑為r，依題意得
，由圓
與直線
相切于點
推出
，列出方程即可求得a，b，利用兩點間距離公式可求得r，即可寫出圓C的方程；(2)求出圓心到直線的距離，分類討論，當直線斜率不存在時方程為滿足題意，當直線斜率存在時設直線方程為
，利用圓心到直線的距離列出方程即可求出k.
(1)設圓心為，半徑為r，依題意，，
直線
的斜率
，
因為圓與直線相切于點，所以
，故，
所以
，解得
，
，
圓C的方程為：；
(2)因為直線l被圓截得弦長為
，所以圓心到直線的距離為
，
①若直線l的斜率不存在，則直線l的方程為：，經驗證滿足題意；
②若直線l的斜率存在，則設直線l的方程為：，
圓心
到直線l的距離為
，
直線l的方程為：.
綜上，直線l的方程為：或.
科目：高中數學 來源： 題型：
【題目】如圖所示的某種容器的體積為
，它是由圓錐和圓柱兩部分連結而成的，圓柱與圓錐的底面圓半徑都為
.圓錐的高為
，母線與底面所成的角為
；圓柱的高為
.已知圓柱底面造價為
元
，圓柱側面造價為
元，圓錐側面造價為
元.
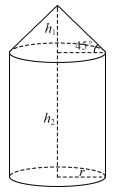
（1）將圓柱的高
表示為底面圓半徑
的函數，并求出定義域；
（2）當容器造價最低時，圓柱的底面圓半徑為多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以下命題中：
①若向量
、
、
是空間的一組基底，則向量
、
、也是空間的一組基底；
②已知
、
、
三點不共線，點
為平面
外任意一點，若點
滿足
，則點
平面；
③曲線
與曲線
（
且
）有相同的焦點.
④過定圓
上一定點
作圓的動弦
，為坐標原點，若
，則動點
的軌跡為橢圓；
⑤若過點
的直線
交橢圓
于不同的兩點
，且是的中點，則直線的方程是
.
其中真命題的序號是______.（寫出所有真命題的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解春季晝夜溫差大小與某種子發芽數之間的關系，現在從4月份的30天中隨機挑選了5天進行研究，且分別記錄了明天晝夜溫差與每天100顆種子浸泡后的發芽數，得到如下表格：
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
溫差x/℃ | 10 | 11 | 13 | 12 | 8 |
發芽數y/顆 | 23 | 25 | 30 | 26 | 16 |
從這5天中任選2天，記發芽的種子數分別為
，求事件“君不小于25”的概率；
（2）從這5天中任選2天，若選取的是4月1日與4月30日的兩組數據，請根據這5填中的另三天的數據，求出
關于
的線性回歸方程，
.
（參考公式：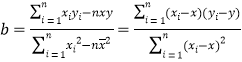
，
）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）一個盒子里裝有三張卡片，分別標記有數字
，
，
，這三張卡片除標記的數字外完全相同。隨機有放回地抽取次，每次抽取張，將抽取的卡片上的數字依次記為
，
，
.
（Ⅰ）求“抽取的卡片上的數字滿足
”的概率；
（Ⅱ）求“抽取的卡片上的數字，，不完全相同”的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將圓
上每一點的橫坐標保持不變，縱坐標變為原來的2倍，得曲線C.
（1）寫出C的參數方程；
（2）設直線
與C的交點為
，以坐標原點為極點，x軸正半軸為極坐標建立極坐標系，求過線段
的中點且與
垂直的直線的極坐標方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個大型噴水池的中央有一個強力噴水柱，為了測量噴水柱噴出的水柱的高度，某人在噴水柱正西方向的點A測得水柱頂端的仰角為45°，沿點A向北偏東30°前進100 m到達點B，在B點測得水柱頂端的仰角為30°，則水柱的高度是( )
A. 50 mB. 100 m
C. 120 mD. 150 m
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P-ABCD中，底面ABCD為正方形，平面PAD⊥平面ABCD，點M在線段PPD//平面MAC，PA=PD=
，AB=4．
（I）求證：M為PB的中點；
（II）求二面角B-PD-A的大小；
（III）求直線MC與平面BDP所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線方程為y2＝－4x，直線l的方程為2x＋y－4＝0，在拋物線上有一動點A，點A到y軸的距離為m，到直線l的距離為n，則m＋n的最小值為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com