
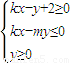 表示的平面區域內部及邊界上運動,
表示的平面區域內部及邊界上運動,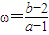 的取值范圍是 .
的取值范圍是 . 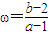 表示Q(1,2)與P(a,b)連線的斜率,利用斜率與傾斜角的關系求PQ斜率的最值,即可得到ω的取值范圍.
表示Q(1,2)與P(a,b)連線的斜率,利用斜率與傾斜角的關系求PQ斜率的最值,即可得到ω的取值范圍.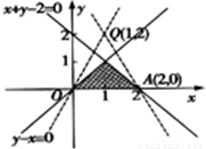
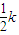 ,-
,-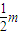 )在直線x-y=0上,∴m=k=-1
)在直線x-y=0上,∴m=k=-1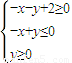 ,
,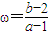 表示直線PQ的斜率
表示直線PQ的斜率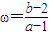 的取值范圍是(-∞,2]∪[2,+∞)
的取值范圍是(-∞,2]∪[2,+∞)

科目:高中數學 來源: 題型:
| 2 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| f(x) |
| x2 |
| a+b |
| 2 |
| f(b)-f(a) |
| b-a |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| f(a)+f(b) |
| 2 |
| f(b)-f(a) |
| b-a |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com