
【題目】已知函數![]() (a,b∈R).
(a,b∈R).
(1)若f(x)在點(1,f(1))的切線為y=x+1,求f(x)的單調性與極值;
(2)若b=﹣1,函數![]() 有且只有一個零點,求實數a的取值范圍.
有且只有一個零點,求實數a的取值范圍.
【答案】(1)f(x)的單調遞增區間為(![]() ,+∞),單調遞減區間為(0,
,+∞),單調遞減區間為(0,![]() ),f(x)的極小值﹣2ln
),f(x)的極小值﹣2ln![]() ,無極大值;(2)a<0或a=1
,無極大值;(2)a<0或a=1
【解析】
(1)求出導函數![]() ,利用
,利用![]() 和
和![]() 求得
求得![]() ,再由導函數的正負確定單調性;
,再由導函數的正負確定單調性;
(2)由方程![]() 在(0,+∞)上有且只有一個實根,然后分離參數得
在(0,+∞)上有且只有一個實根,然后分離參數得![]() ,設h(x)
,設h(x)![]() ,研究
,研究![]() 的單調性和極值后可得結論.
的單調性和極值后可得結論.
(1)切點(1,f(1))代入切線y=x+1得:f(1)=2,
∴f(1)=1+b=2,∴b=1,
∴f'(x)![]() 2x+1,
2x+1,
又∵f'(1)=1,∴![]() 2+1=1,∴a
2+1=1,∴a![]() ,
,
∴函數f(x)=﹣2lnx+x2+x,其中x>0,
∴f'(x)![]() 2x+1
2x+1![]() 0,解得x
0,解得x![]() ,
,
列表:
x | (0, |
| ( |
f'(x) | ﹣ | 0 | + |
f(x) | 遞減 | 極小值 | 遞增 |
∴f(x)的單調遞增區間為(![]() ,+∞),單調遞減區間為(0,
,+∞),單調遞減區間為(0,![]() ),
),
∴f(x)的極小值為f(![]() )=﹣2ln
)=﹣2ln![]() (
(![]() )2
)2![]() )=﹣2ln
)=﹣2ln![]() ,無極大值;
,無極大值;
(2)若f(x)有且只有一個零點,
即方程![]() 在(0,+∞)上有且只有一個實根,
在(0,+∞)上有且只有一個實根,
分離參數得![]() ,設h(x)
,設h(x)![]() ,則h'(x)
,則h'(x)![]() ,
,
又設φ(x)=1﹣x﹣2lnx,φ'(x)=﹣1![]() 0,而φ(1)=0,
0,而φ(1)=0,
∴當x∈(0,1)時,h'(x)>0,h(x)單調遞增;當x∈(1,+∞)時,h'(x)<0,h(x)單調遞減,
∴h(x)max=h(1)=1,
又x∈(0,+∞)時恒有h(x)>0,且x趨近于+∞時,h(x)趨近于0,
h(![]() )=e﹣e2<0,且x趨近于0時,h(x)趨近于﹣∞,
)=e﹣e2<0,且x趨近于0時,h(x)趨近于﹣∞,
從而![]() 0或
0或![]() ,
,
即a<0或a=1時函數f(x)有且只有一個零點.


科目:高中數學 來源: 題型:
【題目】天干地支紀年法,源于中國,中國自古便有十天干與十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支紀年法是按順序以一個天干和一個地支相配,排列起來,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年為“甲子”,第二年為“乙丑”,第三年為“丙寅”,…,以此類推,排列到“癸酉”后,天干回到“甲”重新開始,即“甲戌”,“乙亥”,之后地支回到“子”重新開始,即“丙子”,…,以此類推,已知2016年為丙申年,那么到改革開放100年時,即2078年為________年
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() 是正三角形,
是正三角形,![]() 為
為![]() 的中點,平面
的中點,平面![]() 平面
平面![]() .
.
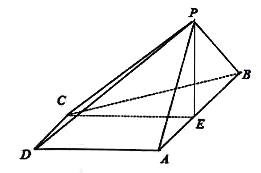
(1)求證:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為:![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為:
的極坐標方程為:![]() .
.
(Ⅰ)求直線![]() 與曲線
與曲線![]() 公共點的極坐標;
公共點的極坐標;
(Ⅱ)設過點![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數h(x)是定義在(﹣2,2)上,滿足h(﹣x)=﹣h(x),且x∈(0,2)時,h(x)=﹣2x,當x∈(﹣2,0)時,不等式[h(x)+2]2>h(x)m﹣1恒成立,則實數m的取值范圍是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() 與
與![]() 的交點
的交點![]() 恰好是
恰好是![]() 中點,又
中點,又![]() ,
,![]() .
.
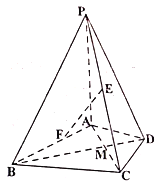
(1)求證:![]() ;
;
(2)設![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上,若直線
上,若直線![]() 平面
平面![]() ,求
,求![]() 的長;
的長;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() ),其中離心率
),其中離心率![]() ,點
,點![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 為橢圓的左右焦點,若
為橢圓的左右焦點,若![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,點
兩點,點![]() 是橢圓
是橢圓![]() 的上頂點,若
的上頂點,若![]() ,試問直線
,試問直線![]() 是否經過定點,若經過定點,求出定點坐標,否則說明理由.
是否經過定點,若經過定點,求出定點坐標,否則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是R上的偶函數,對于
是R上的偶函數,對于![]() 都有
都有![]() 成立,且
成立,且![]() ,當
,當![]() ,且
,且![]() 時,都有
時,都有![]() .則給出下列命題:
.則給出下列命題:
①![]() ;
;
②函數![]() 圖象的一條對稱軸為
圖象的一條對稱軸為![]() ;
;
③函數![]() 在[﹣9,﹣6]上為減函數;④方程
在[﹣9,﹣6]上為減函數;④方程![]() 在[﹣9,9]上有4個根;
在[﹣9,9]上有4個根;
其中正確的命題序號是___________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣ax+1(a∈R).
(1)求f(x)的單調區間;
(2)設g(x)=lnx![]() ,若對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求實數a的取值范圍.
,若對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com