
【題目】已知函數![]() ,
,![]() .
.
(1)當![]() 時,求
時,求![]() 的最小值;
的最小值;
(2)當![]() 時,若存在
時,若存在![]() ,使得對任意的
,使得對任意的![]() ,都有
,都有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析 (2)![]()
【解析】
(1)求出![]() ,分三種情況討論
,分三種情況討論![]() 的范圍,在定義域內,分別令
的范圍,在定義域內,分別令![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,
增區間,![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間,根據單調性;(2)存在
的減區間,根據單調性;(2)存在![]() ,使得對任意的
,使得對任意的![]() 都有
都有![]() 恒成立,等價于
恒成立,等價于![]() ,分別利用導數研究函數的單調性,并求出
,分別利用導數研究函數的單調性,并求出![]() 的最小值,解不等式即可得結果.
的最小值,解不等式即可得結果.
(1)因為![]() 的定義域為
的定義域為![]() ,
,![]()
![]() .
.
①當![]() 時,因為
時,因為![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上為增函數,
上為增函數,![]() ;
;
②當![]() 時,
時,![]() 在
在![]() 上為減函數,在
上為減函數,在![]() 上為增函數,
上為增函數,![]() ;
;
③當![]() 時,
時,![]() 在
在![]() 上為減函數,
上為減函數,![]()
![]() .
.
(2)當![]() 時,若存在
時,若存在![]() ,使得對任意的
,使得對任意的![]() 都有
都有![]() 恒成立,
恒成立,
則![]() .
.
由(1)知,當![]() 時,
時,![]()
![]() .
.
因為![]() ,令
,令![]() ,則
,則![]() ,
,
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,![]() ,所以
,所以![]() 在
在![]() 上單調遞增.
上單調遞增.
所以![]() ,則
,則![]() ,
,
解得![]() ,又
,又![]() ,
,![]() ,
,
所以![]() ,即實數
,即實數![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】一只藥用昆蟲的產卵數![]() 與一定范圍內與溫度
與一定范圍內與溫度![]() 有關, 現收集了該種藥用昆蟲的6組觀測數據如下表:
有關, 現收集了該種藥用昆蟲的6組觀測數據如下表:
溫度 | 21 | 23 | 24 | 27 | 29 | 32 |
產卵數 | 6 | 11 | 20 | 27 | 57 | 77 |
(1)若用線性回歸模型,求![]() 關于
關于![]() 的回歸方程
的回歸方程![]() =
=![]() x+
x+![]() (精確到0.1);
(精確到0.1);
(2)若用非線性回歸模型求![]() 關
關![]() 的回歸方程為
的回歸方程為![]()
![]() 且相關指數
且相關指數![]()
( i )試與 (1)中的線性回歸模型相比,用![]() 說明哪種模型的擬合效果更好.
說明哪種模型的擬合效果更好.
( ii )用擬合效果好的模型預測溫度為![]() 時該種藥用昆蟲的產卵數(結果取整數).
時該種藥用昆蟲的產卵數(結果取整數).
附:一組數據(x1,y1), (x2,y2), ...,(xn,yn), 其回歸直線![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估計為
的斜率和截距的最小二乘估計為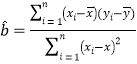 ,
,![]() ,相關指數
,相關指數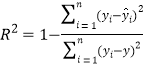 .
.
![]()
![]()
![]()
![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠家擬舉行促銷活動,經調查測算,該產品的年銷售量(即該廠的年產量)![]() 萬件與年促銷費用
萬件與年促銷費用![]() 萬元(
萬元(![]() )滿足
)滿足![]() (
(![]() 為常數),如果不搞促銷活動,則該產品的年銷售量只能是1萬件.已知年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品年平均成本的1.5倍(產品成本包括固定投入和再投入兩部分資金).
為常數),如果不搞促銷活動,則該產品的年銷售量只能是1萬件.已知年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品年平均成本的1.5倍(產品成本包括固定投入和再投入兩部分資金).
(1)將該產品的年利潤![]() 萬元表示為年促銷費用
萬元表示為年促銷費用![]() 萬元的函數;
萬元的函數;
(2)該廠家年促銷費用投入多少萬元時,廠家的利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設F1,F2分別是橢圓E: ![]() (a>b>0)的左、右焦點,過點F1的直線交橢圓E于A,B兩點,|AF1|=3|BF1|,若cos∠AF2B=
(a>b>0)的左、右焦點,過點F1的直線交橢圓E于A,B兩點,|AF1|=3|BF1|,若cos∠AF2B=![]() ,則橢圓E的離心率為( )
,則橢圓E的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義滿足不等式|x![]() A|<B(A∈R,B>0)的實數x的集合叫做A的B鄰域.若a+b
A|<B(A∈R,B>0)的實數x的集合叫做A的B鄰域.若a+b![]() t(t為正常數)的a+b鄰域是一個關于原點對稱的區間,則a2+b2的最小值為______.
t(t為正常數)的a+b鄰域是一個關于原點對稱的區間,則a2+b2的最小值為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為偶函數,函數
為偶函數,函數![]() 為奇函數。
為奇函數。![]() 對任意實數x恒成立.
對任意實數x恒成立.
(1)求函數![]() 與
與![]() ;
;
(2)設![]() ,
,![]() ,若
,若![]() 對于
對于![]() 恒成立,求實數m的取值范圍;
恒成立,求實數m的取值范圍;
(3)對于(2)中的函數![]() ,若方程
,若方程![]() 沒有實數解,實數m的取值范圍.
沒有實數解,實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
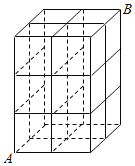
【題目】如圖,某建筑工地搭建的腳手架局部類似于一個![]() 的長方體框架,一個建筑工人欲從
的長方體框架,一個建筑工人欲從![]() 處沿腳手架攀登至
處沿腳手架攀登至 ![]() 處,則其最近的行走路線中不連續向上攀登的概率為( )
處,則其最近的行走路線中不連續向上攀登的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com