
| A. | 函數f(x)的最小正周期為$\frac{π}{2}$ | |
| B. | 函數f(x)的圖象關于y軸對稱 | |
| C. | 點$(\frac{π}{6},0)$為函數f(x)圖象的一個對稱中心 | |
| D. | 函數f(x)的最大值為$\frac{1}{2}$ |
分析 化函數f(x)為正弦型函數,再依次判斷選項中的命題是否正確.
解答 解:函數f(x)=$\frac{{\sqrt{3}}}{2}sin(2x+\frac{π}{3})-{cos^2}x+\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$(sin2xcos$\frac{π}{3}$+cos2xsin$\frac{π}{3}$)-$\frac{1+cos2x}{2}$+$\frac{1}{2}$
=$\frac{\sqrt{3}}{4}$sin2x+$\frac{1}{4}$cos2x
=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)(x∈R),
由ω=2知,f(x)的最小正周期為π,A錯誤;
由f(0)=$\frac{1}{2}$sin$\frac{π}{6}$=$\frac{1}{4}$不是最值,
∴f(x)的圖象不關于y軸對稱,B錯誤;
由f($\frac{π}{6}$)=$\frac{1}{2}$sin$\frac{π}{2}$=$\frac{1}{2}$≠0,
∴點$(\frac{π}{6},0)$不是函數f(x)圖象的一個對稱中心,C錯誤;
由sin(2x+$\frac{π}{6}$)∈[-1,1],∴f(x)的最大值是$\frac{1}{2}$,D正確.
故選:D.
點評 本題考查了三角函數的圖象與性質的應用問題,是基礎題.


科目:高中數學 來源: 題型:解答題
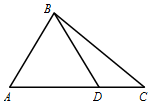 在△ABC中(圖),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7}$,線段AC上點D滿足AD=2DC.
在△ABC中(圖),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7}$,線段AC上點D滿足AD=2DC.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | $±\sqrt{3}$ | C. | 2 | D. | $±\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3種 | B. | 6種 | C. | 9種 | D. | 18種 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {1} | B. | {-1,0} | C. | {-1,0,1} | D. | ∅ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com