解:(1)由3x+5≠0且
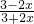
>0,解得x≠-

且-

<x<

.取交集得-

<x<

.
(2)令μ(x)=3x+5,隨著x增大,函數值減小,所以在定義域內是減函數;
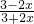
=-1+

隨著x增大,函數值減小,所以在定義域內是減函數.
又y=lgx在定義域內是增函數,根據復合函數的單調性可知,y=
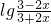
是減函數,所以f(x)=
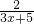
+
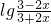
是減函數.
(3)因為直接求f(x)的反函數非常復雜且不易求出,于是利用函數與其反函數之間定義域與值域的關系求解.
設函數f(x)的反函數f
-1(x)與x軸的交點為(x
0,0).根據函數與反函數之間定義域與值域的關系可知,f(x)與y軸的交點是(0,x
0),將(0,x
0)代入f(x),解得x
0=

.
所以函數y=f
-1(x)的圖象與x軸有交點,交點為(

,0).
分析:(1)讓分母不為0且真數大于0求解即可.
(2)把f(x)分成兩個函數,分別求單調性,再利用復合函數的單調性即可.
(3)利用函數與其反函數之間定義域與值域的關系,把函數y=f
-1(x)的圖象與x軸有無交點的問題轉化為f(x)與y軸的交點問題即可.
點評:本題綜合考查了函數的定義域,單調性和互為反函數的兩函數之間的關系.在求復合函數的單調性時,遵循的原則是單調性相同復合函數為增函數,單調性相反復合函數為減函數.

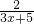 +
+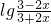 ,
,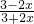 >0,解得x≠-
>0,解得x≠- 且-
且- <x<
<x< .取交集得-
.取交集得- <x<
<x< .
.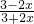 =-1+
=-1+ 隨著x增大,函數值減小,所以在定義域內是減函數.
隨著x增大,函數值減小,所以在定義域內是減函數.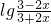 是減函數,所以f(x)=
是減函數,所以f(x)=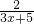 +
+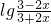 是減函數.
是減函數. .
. ,0).
,0).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案