【題目】下列函數(shù)中，在區(qū)間（0，2）上為增函數(shù)的是（ ）
A.y=3﹣x
B.y=x2+1
C.y= 
D.y=﹣x2+1
【答案】B
【解析】解：若y=3﹣x，則y′=﹣1＜0在區(qū)間（0，2）上恒成立，故區(qū)間（0，2）上，函數(shù)為減函數(shù)；
若y=x2+1，則y′=2x＞0在區(qū)間（0，2）上恒成立，故區(qū)間（0，2）上，函數(shù)為增函數(shù)；
若y= 
，則y′=﹣ 
＜0在區(qū)間（0，2）上恒成立，故區(qū)間（0，2）上，函數(shù)為減函數(shù)；
若y=﹣x2+1，則y′=﹣2x＜0在區(qū)間（0，2）上恒成立，故區(qū)間（0，2）上，函數(shù)為減函數(shù)；
故選：B
【考點精析】本題主要考查了函數(shù)單調(diào)性的判斷方法和利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性的相關(guān)知識點，需要掌握單調(diào)性的判定法：①設(shè)x1,x2是所研究區(qū)間內(nèi)任兩個自變量，且x1＜x2；②判定f(x1)與f(x2)的大小；③作差比較或作商比較；一般的,函數(shù)的單調(diào)性與其導(dǎo)數(shù)的正負(fù)有如下關(guān)系： 在某個區(qū)間
內(nèi)，(1)如果
，那么函數(shù)
在這個區(qū)間單調(diào)遞增；(2)如果
，那么函數(shù)
在這個區(qū)間單調(diào)遞減才能正確解答此題．
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)g（x）=3x ， h（x）=9x ．
（1）解方程：h（x）﹣8g（x）﹣h（1）=0；
（2）令p（x）= 
，求值：p（ 
）+p（ 
）+…+p（ 
）+p（ 
）．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】函數(shù)f（x）=loga（x+1），（a＞0，a≠1）的圖象經(jīng)過點（﹣ 
，﹣2），圖象上有三個點A，B，C，它們的橫坐標(biāo)依次為t﹣1，t，t+1，（t≥1），記三角形ABC的面積為S（t），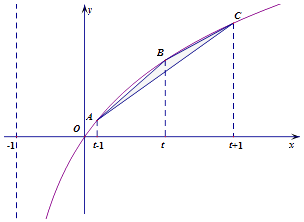 
（1）求f（x）的表達(dá)式；
（2）求S（1）；
（3）是否存在正整數(shù)m，使得對于一切不小于1的t，都有S（t）＜m，若存在求的最小值，若不存在，請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知冪函數(shù)y=x3m﹣9（m∈N*）的圖象關(guān)于y軸對稱，且在（0，+∞）上函數(shù)值隨x增大而減小．
（1）求m的值；
（2）求滿足（a+1） 
＜（3﹣2a） 的a的范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知定義域為R的函數(shù)f（x）= 
是奇函數(shù)．
（1）求a，b的值；
（2）判斷函數(shù)的單調(diào)性并證明；
（3）若對任意的t∈R，不等式f（t2﹣2t）+f（2t2﹣k）＜0恒成立，求k的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某高新技術(shù)公司要生產(chǎn)一批新研發(fā)的
款手機和
款手機，生產(chǎn)一臺
款手機需要甲材料
，乙材料
，并且需要花費1天時間，生產(chǎn)一臺
款手機需要甲材料
，乙材料
，也需要1天時間，已知生產(chǎn)一臺
款手機利潤是1000元，生產(chǎn)一臺
款手機的利潤是2000元，公司目前有甲、乙材料各，則在
不超過120天的情況下，公司生產(chǎn)兩款手機的最大利潤是__________元．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知P（﹣2，3）是函數(shù)y= 
圖象上的點，Q是雙曲線在第四象限這一分支上的動點，過點Q作直線，使其與雙曲線y= 只有一個公共點，且與x軸、y軸分別交于點C、D，另一條直線y= 
x+6與x軸、y軸分別交于點A、B．則
（1）O為坐標(biāo)原點，三角形OCD的面積為 ．
（2）四邊形ABCD面積的最小值為 ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，四棱錐P﹣ABCD中，底面ABCD為平行四邊形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．
（Ⅰ） 證明：PA⊥BD；
（Ⅱ） 設(shè)PD=AD=1，求直線PC與平面ABCD所成角的正切值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)等差數(shù)列{an}的前n項和為Sn ， 已知a3=24，a6=18．
（Ⅰ） 求數(shù)列{an}的通項公式；
（Ⅱ）求數(shù)列{an}的前n項和Sn；
（Ⅲ）當(dāng)n為何值時，Sn最大，并求Sn的最大值．
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com