
【題目】在矩形ABCD中,AB=4 ![]() ,AD=2
,AD=2 ![]() ,將△ABD沿BD折起,使得點A折起至A′,設(shè)二面角A′﹣BD﹣C的大小為θ.
,將△ABD沿BD折起,使得點A折起至A′,設(shè)二面角A′﹣BD﹣C的大小為θ.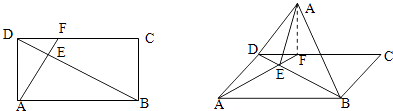
(1)當θ=90°時,求A′C的長;
(2)當cosθ= ![]() 時,求BC與平面A′BD所成角的正弦值.
時,求BC與平面A′BD所成角的正弦值.
【答案】
(1)解:在圖1中,過A作BD的垂線交BD于E,交DC于F,連接CE.
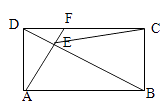
∵AB=4 ![]() ,AD=2
,AD=2 ![]() ,∴BD=
,∴BD= ![]() =10.
=10.
∴ ![]() ,BE=
,BE= ![]() =8,cos∠CBE=
=8,cos∠CBE= ![]() =
= ![]() .
.
在△BCE中,由余弦定理得CE= ![]() =2
=2 ![]() .
.
∵θ=90°,∴A′E⊥平面ABCD,∴A′E⊥CE.
∴|A′C|= ![]() =2
=2 ![]() .
.
(2)DE= ![]() =2.
=2.
∵tan∠FDE= ![]() ,∴EF=1,DF=
,∴EF=1,DF= ![]() =
= ![]() .
.
當 ![]() 即cos∠A′EF=
即cos∠A′EF= ![]() 時,
時, ![]() .
.
∴A′E2=A′F2+EF2,∴∠A'FE=90°
又BD⊥AE,BD⊥EF,∴BD⊥平面A'EF,∴BD⊥A'F
∴A'F⊥平面ABCD.
以F為原點,以FC為x軸,以過F的AD的平行線為y軸,以FA′為z軸建立空間直角坐標系如圖所示:
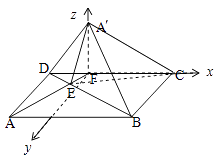
∴A′(0,0, ![]() ),D(﹣
),D(﹣ ![]() ,0,0),B(3
,0,0),B(3 ![]() ,2
,2 ![]() ,0),C(3
,0),C(3 ![]() ,0,0).
,0,0).
∴ ![]() =(0,2
=(0,2 ![]() ,0),
,0), ![]() =(4
=(4 ![]() ,2
,2 ![]() ,0),
,0), ![]() =(
=( ![]() ,0,
,0, ![]() ).
).
設(shè)平面A′BD的法向量為 ![]() =(x,y,z),則
=(x,y,z),則 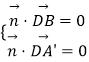 ,
,
∴ ![]() ,令z=1得
,令z=1得 ![]() =(﹣
=(﹣ ![]() ,2
,2 ![]() ,1).
,1).
∴cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() .
.
∴BC與平面A'BD所成角的正弦值為 ![]() .
.
【解析】(1)根據(jù)題意作出輔助線利用勾股定理可得AE、CE再由A′E⊥CE得出結(jié)果。(2)利用余弦定理可得A ' F的值,從而得出A'F⊥平面ABCD,建立空間直角坐標系如圖所示,求出向量CB和平面A′BD的法向量,根據(jù)兩個向量的數(shù)量積公式求出BC與平面A'BD所成角的正弦值即可。
【考點精析】解答此題的關(guān)鍵在于理解空間角的異面直線所成的角的相關(guān)知識,掌握已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則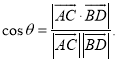 .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩人各射擊一次,擊中目標的概率分別是 ![]() 和
和 ![]() .假設(shè)兩人射擊是否擊中目標,相互之間沒有影響;每人各次射擊是否擊中目標,相互之間也沒有影響.
.假設(shè)兩人射擊是否擊中目標,相互之間沒有影響;每人各次射擊是否擊中目標,相互之間也沒有影響.
(1)求甲射擊4次,至少1次未擊中目標的概率;
(2)求兩人各射擊4次,甲恰好擊中目標2次且乙恰好擊中目標3次的概率;
(3)假設(shè)某人連續(xù)2次未擊中目標,則停止射擊.問:乙恰好射擊5次后,被中止射擊的概率是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知直線l:x+ ![]() y﹣c=0(c>0)為公海與領(lǐng)海的分界線,一艘巡邏艇在O處發(fā)現(xiàn)了北偏東60°海面上A處有一艘走私船,走私船正向停泊在公海上接應(yīng)的走私海輪B航行,以使上海輪后逃竄.已知巡邏艇的航速是走私船航速的2倍,且兩者都是沿直線航行,但走私船可能向任一方向逃竄.
y﹣c=0(c>0)為公海與領(lǐng)海的分界線,一艘巡邏艇在O處發(fā)現(xiàn)了北偏東60°海面上A處有一艘走私船,走私船正向停泊在公海上接應(yīng)的走私海輪B航行,以使上海輪后逃竄.已知巡邏艇的航速是走私船航速的2倍,且兩者都是沿直線航行,但走私船可能向任一方向逃竄. 
(1)如果走私船和巡邏船相距6海里,求走私船能被截獲的點的軌跡;
(2)若O與公海的最近距離20海里,要保證在領(lǐng)海內(nèi)捕獲走私船(即不能截獲走私船的區(qū)域與公海不想交).則O,A之間的最遠距離是多少海里?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】閱讀材料:根據(jù)兩角和與差的正弦公式,有: sin(α+β)=sinαcosβ+cosαsinβ﹣﹣﹣﹣﹣﹣①
sin(α﹣β)=sinαcosβ﹣cosαsinβ﹣﹣﹣﹣﹣﹣②
由①+②得sin(α+β)+sin(α﹣β)=2sinαcosβ﹣﹣﹣﹣﹣﹣③
令α+β=A,α﹣β=β 有α= ![]() ,β=
,β= ![]() 代入③得 sinA+sinB=2sin
代入③得 sinA+sinB=2sin ![]() cos
cos ![]() .
.
(1)利用上述結(jié)論,試求sin15°+sin75°的值;
(2)類比上述推證方法,根據(jù)兩角和與差的余弦公式,證明:cosA﹣cosB=﹣2sin ![]() cos
cos ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,點P在正方體ABCD﹣A1B1C1D1的表面上運動,且P到直線BC與直線C1D1的距離相等,如果將正方體在平面內(nèi)展開,那么動點P的軌跡在展開圖中的形狀是( )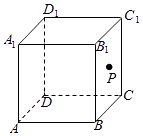
A.
B.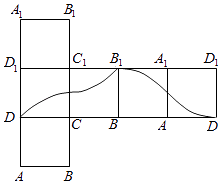
C.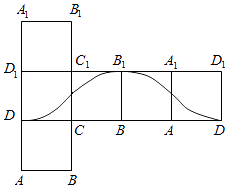
D.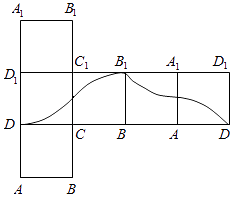
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=sin(ωx+φ)(ω>0,0<φ<π)的圖象與 ![]() 的圖象的對稱軸相同,則f(x)的一個遞增區(qū)間為( )
的圖象的對稱軸相同,則f(x)的一個遞增區(qū)間為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖:在四棱錐E﹣ABCD中,CB=CD=CE=1,AB=AD=AE= ![]() ,EC⊥BD,底面四邊形是個圓內(nèi)接四邊形,且AC是圓的直徑.
,EC⊥BD,底面四邊形是個圓內(nèi)接四邊形,且AC是圓的直徑.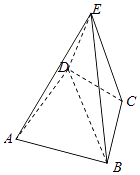
(1)求證:平面BED⊥平面ABCD;
(2)點P是平面ABE內(nèi)一點,滿足DP∥平面BEC,求直線DP與平面ABE所成角的正弦值的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若對任意的x∈D,均有g(shù)(x)≤f(x)≤h(x)成立,則稱函數(shù)f(x)為函數(shù)g(x)到函數(shù)h(x)在區(qū)間D上的“任性函數(shù)”.已知函數(shù)f(x)=kx,g(x)=x2﹣2x,h(x)=(x+1)(lnx+1),且f(x)是g(x)到h(x)在區(qū)間[1,e]上的“任性函數(shù)”,則實數(shù)k的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于n維向量A=(a1 , a2 , …,an),若對任意i∈{1,2,…,n}均有ai=0或ai=1,則稱A為n維T向量.對于兩個n維T向量A,B,定義 ![]() .
.
(1)若A=(1,0,1,0,1),B=(0,1,1,1,0),求d(A,B)的值.
(2)現(xiàn)有一個5維T向量序列:A1 , A2 , A3…,若A1=(1,1,1,1,1)且滿足:d(Ai , Ai+1)=2,i∈N* . 求證:該序列中不存在5維T向量(0,0,0,0,0).
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com